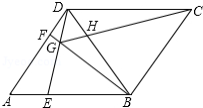
如图,已知 的半径为1, , 是 的两条弦,且 ,延长 交 于点 ,连接 , ,若 ,则 .
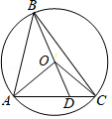
如图,平行四边形纸片 的边 , 的长分别是 和 ,将其四个角向内对折后,点 与点 重合于点 ,点 与点 重合于点 .四条折痕围成一个“信封四边形” ,其顶点分别在平行四边形 的四条边上,则 .
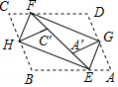
如图,已知正方形 的边长为3, 、 分别是 、 边上的点,且 ,将 绕点 逆时针旋转 ,得到 .若 ,则 的长为 .

如图,已知正方形 的边长为5,点 、 分别在 、 上, , 与 相交于点 ,点 为 的中点,连接 ,则 的长为 .

如图,矩形 的四个顶点分别在矩形 的各条边上, , , .有以下四个结论:① ;② ;③ ;④矩形 的面积是 .其中一定成立的是 .(把所有正确结论的序号填在横线上)

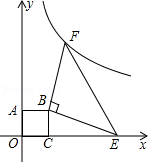
如图,在平面直角坐标系中,经过点 的双曲线 同时经过点 ,且点 在点 的左侧,点 的横坐标为 , ,则 的值为 .
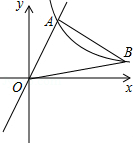
如图,四边形 为正方形, 是等腰直角三角形, ,点 , 在 轴上,点 在 轴上,点 在双曲线 第一象限内的图象上, , ,则 .
如图,一只蚂蚁在正方形 区域内爬行,点 是对角线的交点, , , 分别交线段 , 于 , 两点,则蚂蚁停留在阴影区域的概率为 .

如图,点 的坐标为 ,作 轴, 轴,垂足分别为 , ,点 为线段 的中点,点 从点 出发,在线段 、 上沿 运动,当 时,点 的坐标为 .

如图,在菱形 中, ,点 、 分别是 、 上任意的点(不与端点重合),且 ,连接 与 相交于点 ,连接 与 相交于点 ,给出如下几个结论:
(1) ;
(2) 与 一定不垂直;
(3) 的大小为定值;
(4) ;
(5)若 ,则 .
其中正确结论的序号为 .