如图,将矩形 沿对角线 折叠,点 落在点 处, 交 于点 ,已知 ,则 的度数为

A. B. C. D.
如图,将一张三角形纸片 的一角折叠,使点 落在 外的 处,折痕为 .如果 , , ,那么下列式子中正确的是

A. B. C. D.
如图,直线 ,点 是直线 上一点,点 是直线 外一点,若 , ,则 的度数是
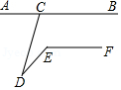
A. B. C. D.
定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图, 是 的外角.求证: .
| 证法1:如图, (三角形内角和定理), 又 (平角定义), (等量代换). (等式性质). |
| 证法2:如图, , , 且 (量角器测量所得) 又 (计算所得) (等量代换). |
下列说法正确的是

| A. |
证法1还需证明其他形状的三角形,该定理的证明才完整 |
| B. |
证法1用严谨的推理证明了该定理 |
| C. |
证法2用特殊到一般法证明了该定理 |
| D. |
证法2只要测量够一百个三角形进行验证,就能证明该定理 |
如图,等腰直角三角形 中, , ,将 绕点 顺时针旋转 ,得到 ,连结 ,过点 作 交 的延长线于点 ,连结 ,则 的度数

A.随着 的增大而增大B.随着 的增大而减小
C.不变D.随着 的增大,先增大后减小
如图,沿 方向开山修路.为了加快施工进度,要在小山的另一边同时施工,从 上的一点 取 , , .那么另一边开挖点 离 多远正好使 , , 三点在一直线上 取1.732,结果取整数)?

含 角的直角三角板与直线 、 的位置关系如图所示,已知 , ,则

A. B. C. D.