如图,在▱ABCD中,AC为对角线,AC=BC=5,AB=6,AE是△ABC的中线.
(1)用无刻度的直尺画出△ABC的高CH(保留画图痕迹);
(2)求△ACE的面积.
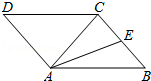
如图, 中, , 为 的角平分线,以点 为圆心, 为半径作 与线段 交于点 .
(1)求证: 为 的切线;
(2)若 , ,求 的长.

如图,在 中, 的垂直平分线交 于点 , 平分 ,若 ,则 的度数为
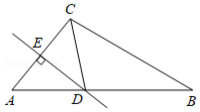
| A. |
|
B. |
|
C. |
|
D. |
|
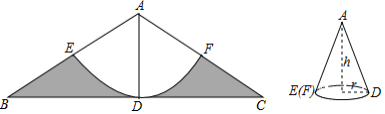
如图,在等腰中,
,
是
的角平分线,且
,以点
为圆心,
长为半径画弧
,交
于点
,交
于点
.
(1)求由弧及线段
、
、
围成图形(图中阴影部分)的面积;
(2)将阴影部分剪掉,余下扇形,将扇形
围成一个圆锥的侧面,
与
正好重合,圆锥侧面无重叠,求这个圆锥的高
.
定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
(1)如图1,在中,
,
是
的角平分线,
,
分别是
,
上的点.
求证:四边形是邻余四边形.
(2)如图2,在的方格纸中,
,
在格点上,请画出一个符合条件的邻余四边形
,使
是邻余线,
,
在格点上.
(3)如图3,在(1)的条件下,取中点
,连结
并延长交
于点
,延长
交
于点
.若
为
的中点,
,
,求邻余线
的长.

请从以下两个小题中任选一个作答,若多选,则按第一题计分.
.如图,在
中,
和
是
的两条角平分线.若
,则
的度数为 .
.(结果精确到

如图,在 中, , , , 的高 与角平分线 交于点 ,则 的值为
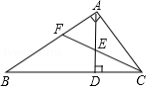
| A. |
|
B. |
|
C. |
|
D. |
|
如图,和
中,
,
,
,边
与边
交于点
(不与点
,
重合),点
,
在
异侧,
为
的内心.
(1)求证:;
(2)设,请用含
的式子表示
,并求
的最大值;
(3)当时,
的取值范围为
,分别直接写出
,
的值.

如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为16cm2,则△BEF的面积: cm2.
