如图,将矩形纸片 折叠 ,使 落在 上, 为折痕,然后将矩形纸片展开铺在一个平面上, 点不动,将 边折起,使点 落在 上的点 处,连接 ,若 , ,则 的长为 .

如图,在矩形 中, , ,点 在线段 上运动(含 、 两点),连接 ,以点 为中心,将线段 逆时针旋转 到 ,连接 ,则线段 的最小值为

| A. |
|
B. |
|
C. |
|
D. |
3 |
如图,在平行四边形 中, 是 的中点,则下列四个结论:
① ;
②若 , ,则 ;
③若 ,则 ;
④若 ,则 与 全等.
其中正确结论的个数为

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
如图,在 中, , ,垂足分别为点 和点 , 与 交于点 ,连接 并延长交 于点 ,若 , , ,则 值为 .

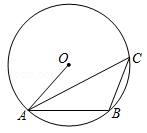
如图, , , 是半径为1的 上的三个点,若 , ,则 的度数为
| A. |
|
B. |
|
C. |
|
D. |
|
研究立体图形问题的基本思路是把立体图形问题转化为平面图形问题.
(1)阅读材料
立体图形中既不相交也不平行的两条直线所成的角,就是将直线平移使其相交所成的角.
例如,正方体 (图 ,因为在平面 中, , 与 相交于点 ,所以直线 与 所成的 就是既不相交也不平行的两条直线 与 所成的角.
解决问题
如图1,已知正方体 ,求既不相交也不平行的两直线 与 所成角的大小.

(2)如图2, , 是正方体相邻两个面上的点;
①下列甲、乙、丙三个图形中,只有一个图形可以作为图2的展开图,这个图形是 ;
②在所选正确展开图中,若点 到 , 的距离分别是2和5,点 到 , 的距离分别是4和3, 是 上一动点,求 的最小值.

如图, 中, , ,点 ,点 ,反比例函数 的图象经过点 .
(1)求反比例函数的解析式;
(2)将直线 向上平移 个单位后经过反比例函数 图象上的点 ,求 , 的值.

如图, 中, , , ,点 为 的中点,以 为圆心,以 为半径作半圆,交 于点 ,则图中阴影部分的面积是 .

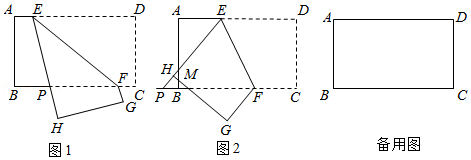
在矩形 中, ,点 、 分别是边 、 上的动点,且 ,连接 ,将矩形 沿 折叠,点 落在点 处,点 落在点 处.
(1)如图1,当 与线段 交于点 时,求证: ;
(2)如图2,当点 在线段 的延长线上时, 交 于点 ,求证:点 在线段 的垂直平分线上;
(3)当 时,在点 由点 移动到 中点的过程中,计算出点 运动的路线长.