已知线段 ,按如下步骤作图:①作射线 ,使 ;②作 的平分线 ;③以点 为圆心, 长为半径作弧,交 于点 ;④过点 作 于点 ,则

| A. |
|
B. |
|
C. |
|
D. |
|
如图, 在 中, ,按下列步骤作图:①以点 为圆心, 适当长为半径画弧, 与 , 分别交于点 , ;②分别以 , 为圆心, 大于 的长为半径画弧, 两弧交于点 ;③作射线 交 于点 ;④过点 作 于点 . 下列结论正确的是
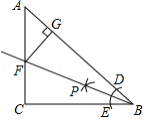
A . B . C . D .
如图,矩形 中, , 相交于点 ,过点 作 交 于点 ,交 于点 ,过点 作 交 于点 ,交 于点 ,连接 , .则下列结论:
① ;
② ;
③ ;
④当 时,四边形 是菱形.
其中,正确结论的个数是

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
如图,在 和 中, , ,添加下列一个条件后,仍然不能证明 ,这个条件是

A. B. C. D.
如图摆放的一副学生用直角三角板, , , 与 相交于点 ,当 时, 的度数是

A. B. C. D.
在勾股定理的学习过程中,我们已经学会了运用如图图形,验证著名的勾股定理,这种根据图形直观推论或验证数学规律和公式的方法,简称为"无字证明".实际上它也可用于验证数与代数,图形与几何等领域中的许多数学公式和规律,它体现的数学思想是
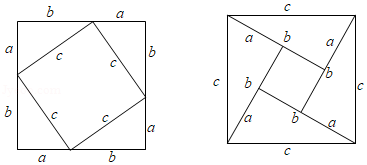
| A. |
统计思想 |
B. |
分类思想 |
C. |
数形结合思想 |
D. |
函数思想 |
如图,在 中,按以下步骤作图:①分别以点 和 为圆心,以大于 的长为半径作弧,两弧相交于点 和 ;②作直线 交 于点 ,连接 .若 , ,则 的长为
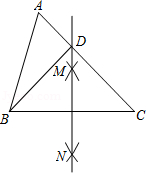
A.2B.3C.4D.6
如图,一次函数 与反比例函数 的图象交于 , 两点,点 在以 为圆心,1为半径的 上, 是 的中点,已知 长的最大值为 ,则 的值为

A. B. C. D.
如图,在矩形 中 , ,将 沿 折叠,使点 恰好落在对角线 上 处,则 的长是

A.3B. C.5D.
如图, 是 的切线,点 为切点, 交 于点 , ,点 在 上, .则 等于
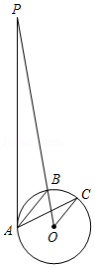
| A. |
|
B. |
|
C. |
|
D. |
|