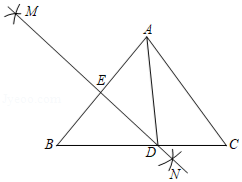
如图,在 中, ,分别以点 , 为圆心,大于 的长为半径画弧,两弧相交于点 和点 ,作直线 分别交 、 于点 和点 ,若 ,则 的度数是
| A. |
|
B. |
|
C. |
|
D. |
|
阅读理解:如果一个正整数 能表示为两个正整数 , 的平方和,即 ,那么称 为广义勾股数,则下面的四个结论:①7不是广义勾股数;②13是广义勾股数;③两个广义勾股数的和是广义勾股数;④两个广义勾股数的积是广义勾股数.依次正确的是
| A. |
②④ |
B. |
①②④ |
C. |
①② |
D. |
①④ |
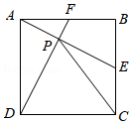
如图,已知 、 分别是正方形 的边 与 的中点, 与 交于 .则下列结论成立的是
| A. |
|
B. |
|
| C. |
|
D. |
|
如图,将一副三角尺按图中所示位置摆放,点 在 上,其中 , , , , ,则 的度数是

| A. |
|
B. |
|
C. |
|
D. |
|
我国古代数学著作《九章算术》中记载了一个问题:"今有池方一丈,葭 jiā 生其中,出水一尺.引葭赴岸,适与岸齐.问水深几何."(丈、尺是长度单位,1丈 尺)其大意为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.水的深度是多少?则水深为

| A. |
10尺 |
B. |
11尺 |
C. |
12尺 |
D. |
13尺 |
如图,在 中, ,按以下步骤作图:①以 为圆心,任意长为半径作弧,分别交 、 于 、 两点;②分别以 、 为圆心,以大于 的长为半径作弧,两弧相交于点 ;③作射线 ,交边 于 点.若 , ,则线段 的长为

| A. |
3 |
B. |
|
C. |
|
D. |
|
如图, 是 的外接圆, 交 于点 ,垂足为点 , , 的延长线交于点 .若 , ,则 的长是

| A. |
10 |
B. |
8 |
C. |
6 |
D. |
4 |
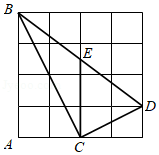
如图,在 的正方形网格中,每个小正方形的边长都为1, 为 与正方形网格线的交点,下列结论正确的是
| A. |
|
B. |
|
C. |
|
D. |
|
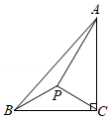
如图, 中, , , .点 为 内一点,且满足 .当 的长度最小时, 的面积是
| A. |
3 |
B. |
|
C. |
|
D. |
|
已知锐角 ,如图,按下列步骤作图:①在 边取一点 ,以 为圆心, 长为半径画 ,交 于点 ,连接 .②以 为圆心, 长为半径画 ,交 于点 ,连接 .则 的度数为
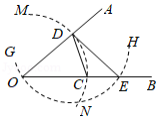
| A. |
|
B. |
|
C. |
|
D. |
|