在 中,若 与 的角平分线交于点 ,则 的形状是
A.锐角三角形B.直角三角形C.钝角三角形D.不能确定
如图,在 中, ,点 是斜边 上一点,且 .
(1)作 的平分线,交 于点 ;(要求尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接 ,求证: .

如图,在 中, 是 边上的高, 平分 交 边于 , , ,则 的大小是
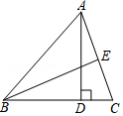
A. B. C. D.
如图,已知平行四边形 ,以点 为圆心,适当长为半径画弧分别交 , 于点 , ,再分别以点 , 为圆心,大于 的长为半径画弧,两弧在 的内部相交于点 ,画射线 交 于 .若 ,则 .

如图,在 中, 是 的平分线, 是外角 的平分线, 与 相交于点 ,若 ,则 是

A. B. C. D.
如图,在 中, , , 的外角 的平分线 交 的延长线于点 .
(1)求 的度数;
(2)过点 作 ,交 的延长线于点 ,求 的度数.

如图, 是 的角平分线,在 上取点 ,使 .
(1)求证: ;
(2)若 , ,求 的度数.

已知: ,求作: 的平分线.作法:①以点 为圆心,适当长为半径画弧,分别交 , 于点 , ;②分别以点 , 为圆心,大于 的长为半径画弧,两弧在 内部交于点 ;③画射线 .射线 即为所求.上述作图用到了全等三角形的判定方法,这个方法是 .
