关于二次函数 的最大值或最小值,下列说法正确的是
| A. |
有最大值4 |
B. |
有最小值4 |
C. |
有最大值6 |
D. |
有最小值6 |
某快递公司在甲地和乙地之间共设有29个服务驿站(包括甲站、乙站),一辆快递货车由甲站出发,依次途经各站驶往乙站,每停靠一站,均要卸下前面各站发往该站的货包各1个,又要装上该站发往后面各站的货包各1个.在整个行程中,快递货车装载的货包数量最多是 个.
已知二次函数 ,当 时 ,则下列说法正确的是
A.当 时, 有最小值B.当 时, 有最大值
C.当 时, 无最小值D.当 时, 有最大值
将一个直角三角形纸片 放置在平面直角坐标系中,点 ,点 ,点 在第一象限, , ,点 在边 上(点 不与点 , 重合).
(Ⅰ)如图①,当 时,求点 的坐标;
(Ⅱ)折叠该纸片,使折痕所在的直线经过点 ,并与 轴的正半轴相交于点 ,且 ,点 的对应点为 ,设 .
①如图②,若折叠后△ 与 重叠部分为四边形, , 分别与边 相交于点 , ,试用含有 的式子表示 的长,并直接写出 的取值范围;
②若折叠后△ 与 重叠部分的面积为 ,当 时,求 的取值范围(直接写出结果即可).

竖直上抛物体离地面的高度 与运动时间 之间的关系可以近似地用公式 表示,其中 是物体抛出时离地面的高度, 是物体抛出时的速度.某人将一个小球从距地面 的高处以 的速度竖直向上抛出,小球达到的离地面的最大高度为
A. B. C. D.
如图,在矩形 中, ,点 在边 上,连接 ,以 为边向右上方作正方形 ,作 ,垂足为 ,连接 .
(1)求证: ;
(2)当 为何值时, 的面积最大?
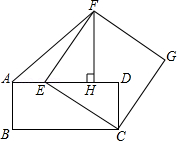
如图,矩形 中, , , 为边 上一个动点,连接 ,取 的中点 ,点 绕点 逆时针旋转 得到点 ,连接 ,则 面积的最小值是

A.4B. C.3D.
二次函数 ,当 且 时, 的最小值为 ,最大值为 ,则 的值为
A. B.2C. D.
已知二次函数 (其中 是自变量),当 时, 随 的增大而增大,且 时, 的最大值为9,则 的值为
A.1或 B. 或 C. D.1
关于二次函数 ,下列说法正确的是
A.图象与 轴的交点坐标为
B.图象的对称轴在 轴的右侧
C.当 时, 的值随 值的增大而减小
D. 的最小值为
如图1,在平面直角坐标系中,直线 分别与 轴、 轴交于点 , , ,等边 的顶点 与原点 重合, 边落在 轴正半轴上,点 恰好落在线段 上,将等边 从图1的位置沿 轴正方向以每秒1个单位长度的速度平移,边 , 分别与线段 交于点 , (如图2所示),设 平移的时间为 .
(1)等边 的边长为 ;
(2)在运动过程中,当 时, 垂直平分 ;
(3)若在 开始平移的同时.点 从 的顶点 出发.以每秒2个单位长度的速度沿折线 运动.当点 运动到 时即停止运动. 也随之停止平移.
①当点 在线段 上运动时,若 与 相似.求 的值;
②当点 在线段 上运动时,设 ,求 与 的函数关系式,并求出 的最大值及此时点 的坐标.

若一次函数 的图象过第一、三、四象限,则二次函数
A.有最大值 .B.有最大值 .C.有最小值 .D.有最小值 .