将一个直角三角形纸片 放置在平面直角坐标系中,点 ,点 ,点 在第一象限, , ,点 在边 上(点 不与点 , 重合).
(Ⅰ)如图①,当 时,求点 的坐标;
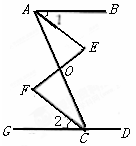
(Ⅱ)折叠该纸片,使折痕所在的直线经过点 ,并与 轴的正半轴相交于点 ,且 ,点 的对应点为 ,设 .
①如图②,若折叠后△ 与 重叠部分为四边形, , 分别与边 相交于点 , ,试用含有 的式子表示 的长,并直接写出 的取值范围;
②若折叠后△ 与 重叠部分的面积为 ,当 时,求 的取值范围(直接写出结果即可).

相关知识点
推荐套卷

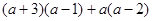

 粤公网安备 44130202000953号
粤公网安备 44130202000953号