若x1、x2是关于一元二次方程ax2+bx+c(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:x1+x2=- ,x1•x2=
,x1•x2=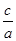 .把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B两个交点间的距离为:AB=|x1-x2|=
.把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B两个交点间的距离为:AB=|x1-x2|=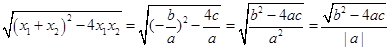 ;
;
参考以上定理和结论,解答下列问题:
设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.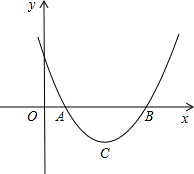
(1)当△ABC为直角三角形时,求b2-4ac的值;
(2)当△ABC为等边三角形时,求b2-4ac的值.
若二次函数 的图象如图所示,则一次函数 与反比例函数 在同一个坐标系内的大致图象为

| A. |
|
B. |
|
| C. |
|
D. |
|
如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:

①abc<0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0
其中正确结论的有( )
| A.①②③ | B.①②④ | C.①③④ | D.②③④ |
平面直角坐标系中,二次函数 的图象如图所示,现给出下列结论:① ;② ;③ ;④ 为实数);⑤ .其中正确结论的个数是

A.2B.3C.4D.5
已知二次函数 的图象如图,则下列哪个选项表示的点有可能在反比例函数 的图象上

A. B. C. D.
(年新疆乌鲁木齐市)如图,抛物线 的对称轴是
的对称轴是 .且过点(
.且过点( ,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是 .(填写正确结论的序号)
,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是 .(填写正确结论的序号)

(2014年山东青岛3分)函数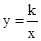 与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
A.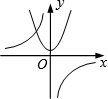 |
B. |
C.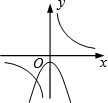 |
D.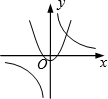 |
(年贵州省毕节)二次函数y=a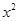 +bx+c的图象如图所示,则下列关系式错误的是( )
+bx+c的图象如图所示,则下列关系式错误的是( )
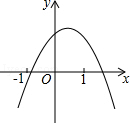
| A.a<0 | B.b>0 | C.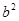 ﹣4ac>0 ﹣4ac>0 |
D.a+b+c<0 |
如图,已知抛物线 , , 为常数, 经过点 ,且对称轴为直线 ,有下列结论:① ;② ;③ ;④无论 , , 取何值,抛物线一定经过 , ;⑤ .其中正确结论有

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
如图,已知抛物线 的对称轴为直线 .给出下列结论:
① ;
② ;
③ ;
④ .
其中,正确的结论有
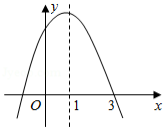
A.1个B.2个C.3个D.4个
如图所示,抛物线 的顶点为 ,与 轴的交点 在点 和 之间,以下结论:
① ;② ;③ ;④
其中正确的有 个.

A.1B.2C.3D.4
已知二次函数 的图象如图所示,以下四个结论:① ;② ;③ ;④ ,正确的是

A.①②B.②④C.①③D.③④