初中数学二次函数的性质填空题

已知函数 $y=-{(x-1)}^2$图象上两点 $A(2,y_1)$， $B(a,y_2)$，其中 $a>2$，则 $y_1$与 $y_2$的大小关系是 $y_1$　　 $y_2$（填“ $<$”、“ $>$”或“ $=$” $)$

已知：二次函数 $y=a{x}^2+\mathit{bx}+c$图象上部分点的横坐标 $x$与纵坐标 $y$的对应值如表格所示，那么它的图象与 $x$轴的另一个交点坐标是　　．

$x$	$\dots$	$-1$	0	1	2	$\dots$
$y$	$\dots$	0	3	4	3	$\dots$

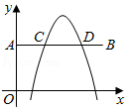
我们定义一种新函数：形如 $y=|a{x}^2+\mathit{bx}+c|(a\ne 0,b^2-4\mathit{ac}>0)$的函数叫做“鹊桥”函数．小丽同学画出了“鹊桥”函数 $y=|x^2-2x-3|$的图象（如图所示），并写出下列五个结论：①图象与坐标轴的交点为 $(-1,0)$， $(3,0)$和 $(0,3)$；②图象具有对称性，对称轴是直线 $x=1$；③当 $-1⩽x⩽1$或 $x⩾3$时，函数值 $y$随 $x$值的增大而增大；④当 $x=-1$或 $x=3$时，函数的最小值是0；⑤当 $x=1$时，函数的最大值是4．其中正确结论的个数是　　．

二次函数 $y=a{x}^2+\mathit{bx}+c$的图象如图所示，若 $M=4a+2b$， $N=a-b$．则 $M$、 $N$的大小关系为 $M$　　 $N$．（填“ $>$”、“ $=$”或“ $<$” $)$

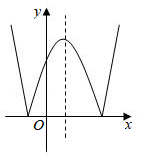
某学习小组为了探究函数 $y＝x^2﹣\left|x\right|$的图象和性质，根据以往学习函数的经验，列表确定了该函数图象上一些点的坐标，表格中的m＝　　．

x	…	﹣2	﹣1.5	﹣1	﹣0.5	0	0.5	1	1.5	2	…
y	…	2	0.75	0	﹣0.25	0	﹣0.25	0	m	2	…

直线 y＝ kx+ b与抛物线 $y=\frac{1}{4}{x}^2$ 交于 A（ x ₁， y ₁）、 B（ x ₂， y ₂）两点，当 OA⊥ OB时，直线 AB恒过一个定点，该定点坐标为 　　．

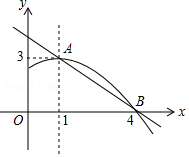
如图是抛物线 $y_1＝a{x}^2+\mathit{bx}+c（a\ne 0）$的图象的一部分，抛物线的顶点坐标是A（1，3），与x轴的一个交点是B（4，0），直线 $y_2＝\mathit{mx}+n（m\ne 0）$与抛物线交于A，B两点，下列结论：

① $\mathit{abc}＞0$；②方程 $a{x}^2+\mathit{bx}+c＝3$有两个相等的实数根；③抛物线与x轴的另一个交点是（﹣1，0）；④当 $1＜x＜4$时，有 $y_2＞y_1$；⑤ $x（\mathit{ax}+b）\le a+b$，其中正确的结论是　　．（只填写序号）

如图，若抛物线y＝ax²+bx+c上的P（4，0），Q两点关于它的对称轴x＝1对称，则Q点的坐标为　　．

已知二次函数 y＝ x ²，当 x＞0时， y随 x的增大而 　　（填"增大"或"减小"）．

已知关于x的二次函数y＝ax²+bx+c的图象经过点 $\mathit{（﹣}2，y_1\mathit{），（﹣}1，y_2）$， $（1，0）$，且 $y_1＜0＜y_2$，对于以下结论：① $\mathit{abc}＞0$；② $a+3b+2c\le 0$；③对于自变量x的任意一个取值，都有 $\frac{a}{b}{x}^2+x⩾-\frac{b}{4a}$；在 $﹣2＜x\mathit{＜﹣}1$中存在一个实数x₀，使得 $x_0=-\frac{a+b}{a}$，中结论错误的是　 （只填写序号）．

如图是二次函数 y＝ ax ²+ bx+ c图象的一部分，图象过点 A（﹣3，0），对称轴为直线 x＝﹣1，给出以下结论：

① abc＜0

② b ²﹣4 ac＞0

③4 b+ c＜0

④若 B（﹣ $\frac{5}{2}$ ， y ₁）、 C（﹣ $\frac{1}{2}$ ， y ₂）为函数图象上的两点，则 y ₁＞ y ₂

⑤当﹣3≤ x≤1时， y≥0，

其中正确的结论是（填写代表正确结论的序号） 　 　．

已知点在抛物线上，当时，总有成立，则的取值范围是　　．

已知函数y＝﹣x²﹣2x，当　　时，函数值y随x的增大而增大．

如图，在平面直角坐标系中，点 $A$的坐标为 $(0,2)$，点 $B$的坐标为 $(4,2)$．若抛物线 $y=-\frac{3}{2}{(x-h)}^2+k(h$、 $k$为常数）与线段 $\mathit{AB}$交于 $C$、 $D$两点，且 $\mathit{CD}=\frac{1}{2}\mathit{AB}$，则 $k$的值为　 　．

二次函数 $y=a{x}^2-3\mathit{ax}+3$ 的图象过点 $A(6,0)$ ，且与 $y$ 轴交于点 $B$ ，点 $M$ 在该抛物线的对称轴上，若 $\mathit{\Delta ABM}$ 是以 $\mathit{AB}$ 为直角边的直角三角形，则点 $M$ 的坐标为