如图,平面直角坐标系 中, 的边 在 轴上,对角线 , 交于点 ,函数 的图象经过点 和点 .
(1)求 的值和点 的坐标;
(2)求 的周长.

如图,双曲线经过矩形
的顶点
,双曲线
交
,
于点
、
,且与矩形的对角线
交于点
,连接
.若
,则
的面积为 .

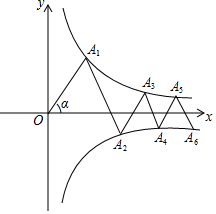
如图,△ ,△ ,△ , 是分别以 , , , 为直角顶点,一条直角边在 轴正半轴上的等腰直角三角形,其斜边的中点 , , , , , , 均在反比例函数 的图象上.则 的值为

| A. |
|
B. |
6 |
C. |
|
D. |
|
从 、2、3、 这四个数中任取两数,分别记为 、 ,那么点 在函数 图象上的概率是
| A. |
|
B. |
|
C. |
|
D. |
|
(1)阅读理解
如图,点,
在反比例函数
的图象上,连接
,取线段
的中点
.分别过点
,
,
作
轴的垂线,垂足为
,
,
,
交反比例函数
的图象于点
.点
,
,
的横坐标分别为
,
,
.
小红通过观察反比例函数的图象,并运用几何知识得出结论:
,
由此得出一个关于,
,
,之间数量关系的命题:
若,则
.
(2)证明命题
小东认为:可以通过“若,则
”的思路证明上述命题.
小晴认为:可以通过“若,
,且
,则
”的思路证明上述命题.
请你选择一种方法证明(1)中的命题.

如图,在平面直角坐标系中,点,
在反比例函数
的图象上运动,且始终保持线段
的长度不变.
为线段
的中点,连接
.则线段
长度的最小值是 (用含
的代数式表示).

如图,点、
、
在反比例函数
的图象上,点
、
、
在反比例函数
的图象上,
,且
,则
为正整数)的纵坐标为 .(用含
的式子表示)
如图,、
两点在反比例函数
的图象上,
、
两点在反比例函数
的图象上,
轴于点
,
轴于点
,
,
,
,则
.

如图,在平面直角坐标系中,矩形 的顶点 , 分别在 轴、 轴上,对角线 轴,反比例函数 的图象经过矩形对角线的交点 .若点 , ,则 的值为

| A. |
16 |
B. |
20 |
C. |
32 |
D. |
40 |
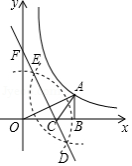
如图,点 在双曲线 上,过点 作 轴,垂足为点 ,分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于 , 两点,作直线 交 轴于点 ,交 轴于点 ,连接 .若 ,则 的值为
| A. |
2 |
B. |
|
C. |
|
D. |
|