已知矩形ABCD的四个顶点均在反比例函数 的图象上,且点A的横坐标是2,则矩形ABCD的面积为 .
已知四个点的坐标分别是 ,
, ,(
),(
),从中随机选取一个点,在反比例函数
图象上的概率是 .
,(
),(
),从中随机选取一个点,在反比例函数
图象上的概率是 .
已知 ( ab≠0且 a≠ b)
(1)化简 A;
(2)若点 P( a, b)在反比例函数 y=﹣ 的图象上,求 A的值.
阅读理解:
材料一:若三个非零实数 , , 满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数 , , 构成"和谐三数组".
材料二:若关于 的一元二次方程 的两根分别为 , ,则有 , .
问题解决:
(1)请你写出三个能构成"和谐三数组"的实数 ;
(2)若 , 是关于 的方程 , , 均不为 的两根, 是关于 的方程 , 均不为 的解.求证: , , 可以构成"和谐三数组";
(3)若 , , 三个点均在反比例函数 的图象上,且三点的纵坐标恰好构成"和谐三数组",求实数 的值.
如图,在平面直角坐标系中,正方形 的顶点 与坐标原点重合,点 的坐标为 ,点 在 轴的正半轴上.直线 分别与边 , 相交于 , 两点,反比例函数 的图象经过点 并与边 相交于点 ,连接 .点 是直线 上的动点,当 时,点 的坐标是 .

如图,平面直角坐标系中,菱形 在第一象限内,边 与 轴平行, , 两点的纵坐标分别为6,4,反比例函数 的图象经过 , 两点,若菱形 的面积为 ,则 的值为 .

阅读理解:
材料一:若三个非零实数 , , 满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数 , , 构成"和谐三数组".
材料二:若关于 的一元二次方程 的两根分别为 , ,则有 , .
问题解决:
(1)请你写出三个能构成"和谐三数组"的实数 ;
(2)若 , 是关于 的方程 , , 均不为 的两根, 是关于 的方程 , 均不为 的解.求证: , , 可以构成"和谐三数组";
(3)若 , , 三个点均在反比例函数 的图象上,且三点的纵坐标恰好构成"和谐三数组",求实数 的值.
如图,矩形 的顶点 在反比例函数 的图象上,点 和点 在 边上, ,连接 , 轴,则 的值为

| A. |
|
B. |
3 |
C. |
4 |
D. |
|
如图,在平面直角坐标系中, 的边 在 轴正半轴上,其中 , ,点 为斜边 的中点,反比例函数 的图象过点 且交线段 于点 ,连接 , ,若 ,则 的值为

| A. |
3 |
B. |
|
C. |
2 |
D. |
1 |
如图,在平面直角坐标系中, 为坐标原点,点 , 在函数 的图象上(点 的横坐标大于点 的横坐标),点 的坐标为 ,过点 作 轴于点 ,过点 作 轴于点 ,连接 , .
(1)求 的值.
(2)若 为 中点,求四边形 的面积.

如图,点在反比例函数
的图象上,且横坐标为1,过点
作两条坐标轴的平行线,与反比例函数
的图象相交于点
、
,则直线
与
轴所夹锐角的正切值为 .

如图,平行四边形 的顶点 在 轴的正半轴上,点 在对角线 上,反比例函数 的图象经过 、 两点.已知平行四边形 的面积是 ,则点 的坐标为
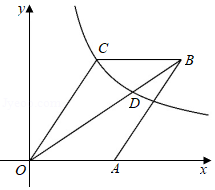
| A. |
|
B. |
, |
C. |
|
D. |
, |