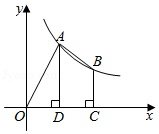
如图,在平面直角坐标系中, 为坐标原点,点 , 在函数 的图象上(点 的横坐标大于点 的横坐标),点 的坐标为 ,过点 作 轴于点 ,过点 作 轴于点 ,连接 , .
(1)求 的值.
(2)若 为 中点,求四边形 的面积.
相关知识点
推荐套卷
如图,在平面直角坐标系中, 为坐标原点,点 , 在函数 的图象上(点 的横坐标大于点 的横坐标),点 的坐标为 ,过点 作 轴于点 ,过点 作 轴于点 ,连接 , .
(1)求 的值.
(2)若 为 中点,求四边形 的面积.
