一大型商场经营某种品牌商品,该商品的进价为每件3元,根据市场调查发现,该商品每周的销售量(件
与售价
(元件)
为正整数)之间满足一次函数关系,下表记录的是某三周的有关数据:
|
4 |
5 |
6 |
|
10000 |
9500 |
9000 |
(1)求与
的函数关系式(不求自变量的取值范围);
(2)在销售过程中要求销售单价不低于成本价,且不高于15元件.若某一周该商品的销售量不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?
(3)抗疫期间,该商场这种商品售价不大于15元件时,每销售一件商品便向某慈善机构捐赠
元
,捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请直接写出
的取值范围.
某文体商店计划购进一批同种型号的篮球和同种型号的排球,每一个排球的进价是每一个篮球的进价的,用3600元购买排球的个数要比用3600元购买篮球的个数多10个.
(1)问每一个篮球、排球的进价各是多少元?
(2)该文体商店计划购进篮球和排球共100个,且排球个数不低于篮球个数的3倍,篮球的售价定为每一个100元,排球的售价定为每一个90元.若该批篮球、排球都能卖完,问该文体商店应购进篮球、排球各多少个才能获得最大利润?最大利润是多少?
黔东南州某超市购进甲、乙两种商品,已知购进3件甲商品和2件乙商品,需60元;购进2件甲商品和3件乙商品,需65元.
(1)甲、乙两种商品的进货单价分别是多少?
(2)设甲商品的销售单价为(单位:元
件),在销售过程中发现:当
时,甲商品的日销售量
(单位:件)与销售单价
之间存在一次函数关系,
、
之间的部分数值对应关系如表:
销售单价 |
11 |
19 |
日销售量 |
18 |
2 |
请写出当时,
与
之间的函数关系式.
(3)在(2)的条件下,设甲商品的日销售利润为元,当甲商品的销售单价
(元
件)定为多少时,日销售利润最大?最大利润是多少?
第33个国际禁毒日到来之际,贵阳市策划了以“健康人生 绿色无毒”为主题的禁毒宣传月活动,某班开展了此项活动的知识竞赛.学习委员为班级购买奖品后与生活委员对话如下:

(1)请用方程的知识帮助学习委员计算一下,为什么说学习委员搞错了;
(2)学习委员连忙拿出发票,发现的确错了,因为他还买了一本笔记本,但笔记本的单价已模糊不清,只能辨认出单价是小于10元的整数,那么笔记本的单价可能是多少元?
为抗击疫情,支持武汉,某物流公司的快递车和货车每天往返于物流公司、武汉两地,快递车比货车多往返一趟,如图表示两车离物流公司的距离(单位:千米)与快递车所用时间
(单位:时)的函数图象,已知货车比快递车早1小时出发,到达武汉后用2小时装卸货物,按原速、原路返回,货车比快递车最后一次返回物流公司晚1小时.
(1)求的函数解析式;
(2)求快递车第二次往返过程中,与货车相遇的时间.
(3)求两车最后一次相遇时离武汉的距离.(直接写出答案)
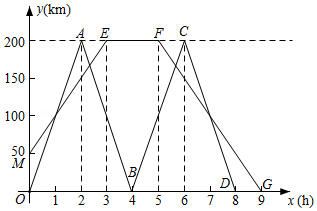
在一条公路上依次有,
,
三地,甲车从
地出发,驶向
地,同时乙车从
地出发驶向
地,到达
地停留0.5小时后,按原路原速返回
地,两车匀速行驶,甲车比乙车晚1.5小时到达
地.两车距各自出发地的路程
(千米)与时间
(小时)之间的函数关系如图所示.请结合图象信息答案下列问题:
(1)甲车行驶速度是 千米1时,,
两地的路程为 千米;
(2)求乙车从地返回
地的过程中,
(千米)与
(小时)之间的函数关系式(不需要写出自变量
的取值范围);
(3)出发多少小时,行驶中的两车之间的路程是15千米?请你直接写出答案.

某商场准备购进、
两种型号电脑,每台
型号电脑进价比每台
型号电脑多500元,用40000元购进
型号电脑的数量与用30000元购进
型号电脑的数量相同,请解答下列问题:
(1),
型号电脑每台进价各是多少元?
(2)若每台型号电脑售价为2500元,每台
型号电脑售价为1800元,商场决定同时购进
,
两种型号电脑20台,且全部售出,请写出所获的利润
(单位:元)与
型号电脑
(单位:台)的函数关系式,若商场用不超过36000元购进
,
两种型号电脑,
型号电脑至少购进10台,则有几种购买方案?
(3)在(2)问的条件下,将不超过所获得的最大利润再次购买,
两种型号电脑捐赠给某个福利院,请直接写出捐赠
,
型号电脑总数最多是多少台.
,
两城市之间有一条公路相连,公路中途穿过
市,甲车从
市到
市,乙车从
市到
市,甲车的速度比乙车的速度慢20千米
时,两车距离
市的路程
(单位:千米)与驶的时间
(单位:小时)的函数图象如图所示,结合图象信息,解答下列问题:
(1)甲车的速度是 千米时,在图中括号内填入正确的数;
(2)求图象中线段所在直线的函数解析式,不需要写出自变量的取值范围;
(3)直接写出甲车出发后几小时,两车距市的路程之和是460千米.

期中考试后,某班班主任对在期中考试中取得优异成绩的同学进行表彰.她到商场购买了甲、乙两种笔记本作为奖品,购买甲种笔记本15个,乙种笔记本20个,共花费250元.已知购买一个甲种笔记本比购买一个乙种笔记本多花费5元.
(1)求购买一个甲种、一个乙种笔记本各需多少元?
(2)两种笔记本均受到了获奖同学的喜爱,班主任决定在期末考试后再次购买两种笔记本共35个,正好赶上商场对商品价格进行调整,甲种笔记本售价比上一次购买时减价2元,乙种笔记本按上一次购买时售价的8折出售.如果班主任此次购买甲、乙两种笔记本的总费用不超过上一次总费用的,求至多需要购买多少个甲种笔记本?并求购买两种笔记本总费用的最大值.
随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少
,求:
(1)型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批型车和新款
型车共60辆,且
型车的进货数量不超过
型车数量的两倍.已知
型车和
型车的进货价格分别为1500元和1800元,计划
型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
倡导垃圾分类,共享绿色生活.为了对回收的垃圾进行更精准的分类,某机器人公司研发出型和
型两款垃圾分拣机器人,已知2台
型机器人和5台
型机器人同时工作
共分拣垃圾3.6吨,3台
型机器人和2台
型机器人同时工作
共分拣垃圾8吨.
(1)1台型机器人和1台
型机器人每小时各分拣垃圾多少吨?
(2)某垃圾处理厂计划向机器人公司购进一批型和
型垃圾分拣机器人,这批机器人每小时一共能分拣垃圾20吨.设购买
型机器人
台
,
型机器人
台,请用含
的代数式表示
;
(3)机器人公司的报价如下表:
型号 |
原价 |
购买数量少于30台 |
购买数量不少于30台 |
|
20万元 |
原价购买 |
打九折 |
|
12万元 |
原价购买 |
打八折 |
在(2)的条件下,设购买总费用为万元,问如何购买使得总费用
最少?请说明理由.
某水果市场销售一种香蕉.甲店的香蕉价格为4元;乙店的香蕉价格为5元
,若一次购买
以上,超过
部分的价格打7折.
(1)设购买香蕉,付款金额
元,分别就两店的付款金额写出
关于
的函数解析式;
(2)到哪家店购买香蕉更省钱?请说明理由.
天水市某商店准备购进、
两种商品,
种商品每件的进价比
种商品每件的进价多20元,用2000元购进
种商品和用1200元购进
种商品的数量相同.商店将
种商品每件的售价定为80元,
种商品每件的售价定为45元.
(1)种商品每件的进价和
种商品每件的进价各是多少元?
(2)商店计划用不超过1560元的资金购进、
两种商品共40件,其中
种商品的数量不低于
种商品数量的一半,该商店有几种进货方案?
(3)“五一”期间,商店开展优惠促销活动,决定对每件种商品售价优惠
元,
种商品售价不变,在(2)的条件下,请设计出
的不同取值范围内,销售这40件商品获得总利润最大的进货方案.
端午节前夕,某商铺用620元购进50个肉粽和30个蜜枣粽,肉粽的进货单价比蜜枣粽的进货单价多6元.
(1)肉粽和蜜枣粽的进货单价分别是多少元?
(2)由于粽子畅销,商铺决定再购进这两种粽子共300个,其中肉粽数量不多于蜜枣粽数量的2倍,且每种粽子的进货单价保持不变,若肉粽的销售单价为14元,蜜枣粽的销售单价为6元,试问第二批购进肉粽多少个时,全部售完后,第二批粽子获得利润最大?第二批粽子的最大利润是多少元?
《人民日报》点赞湖北宜昌“智慧停车平台”.作为“全国智慧城市”试点,我市通过“互联网”、“大数据”等新科技,打造“智慧停车平台”,着力化解城市“停车难”问题.市内某智慧公共停车场的收费标准是:停车不超过30分钟,不收费;超过30分钟,不超过60分钟,计1小时,收费3元;超过1小时后,超过1小时的部分按每小时2元收费(不足1小时,按1小时计).
(1)填空:若市民张先生某次在该停车场停车2小时10分钟,应交停车费 元.若李先生也在该停车场停车,支付停车费11元,则停车场按 小时(填整数)计时收费.
(2)当取整数且
时,求该停车场停车费
(单位:元)关于停车计时
(单位:小时)的函数解析式.