初中数学一次函数的应用试题

某通讯公司就上宽带网推出 $A$， $B$， $C$三种月收费方式．这三种收费方式每月所需的费用 $y$（元 $)$与上网时间 $x\left(h\right)$的函数关系如图所示，则下列判断错误的是 $($　　 $)$

A．每月上网时间不足 $25h$时，选择 $A$方式最省钱

B．每月上网费用为60元时， $B$方式可上网的时间比 $A$方式多

C．每月上网时间为 $35h$时，选择 $B$方式最省钱

D．每月上网时间超过 $70h$时，选择 $C$方式最省钱

某水果店以每千克8元的价格购进苹果若干千克，销售了部分苹果后，余下的苹果每千克降价4元销售，全部售完．销售金额 $y$（元 $)$与销售量 $x$（千克）之间的关系如图所示，请根据图象提供的信息完成下列问题：

（1）降价前苹果的销售单价是　     　元 $/$千克；

（2）求降价后销售金额 $y$（元 $)$与销售量 $x$（千克）之间的函数解析式，并写出自变量的取值范围；

（3）该水果店这次销售苹果盈利了多少元？

小刚去超市购买画笔，第一次花60元买了若干支 $A$ 型画笔，第二次超市推荐了 $B$ 型画笔，但 $B$ 型画笔比 $A$ 型画笔的单价贵2元，他又花100元买了相同支数的 $B$ 型画笔．

（1）超市 $B$ 型画笔单价多少元？

（2）小刚使用两种画笔后，决定以后使用 $B$ 型画笔，但感觉其价格稍贵，和超市沟通后，超市给出以下优惠方案：一次购买不超过20支，则每支 $B$ 型画笔打九折；若一次购买超过20支，则前20支打九折，超过的部分打八折．设小刚购买的 $B$ 型画笔 $x$ 支，购买费用为 $y$ 元，请写出 $y$ 关于 $x$ 的函数关系式．

（3）在（2）的优惠方案下，若小刚计划用270元购买 $B$ 型画笔，则能购买多少支 $B$ 型画笔？

某周日上午 $8:00$小宇从家出发，乘车1小时到达某活动中心参加实践活动． $11:00$时他在活动中心接到爸爸的电话，因急事要求他在 $12:00$前回到家，他即刻按照来活动中心时的路线，以5千米 $/$小时的平均速度快步返回．同时，爸爸从家沿同一路线开车接他，在距家20千米处接上了小宇，立即保持原来的车速原路返回．设小宇离家 $x$（小时）后，到达离家 $y$（千米）的地方，图中折线 $\mathit{OABCD}$表示 $y$与 $x$之间的函数关系．

（1）活动中心与小宇家相距　   　千米，小宇在活动中心活动时间为　 　小时，他从活动中心返家时，步行用了　    　小时；

（2）求线段 $\mathit{BC}$所表示的 $y$（千米）与 $x$（小时）之间的函数关系式（不必写出 $x$所表示的范围）；

（3）根据上述情况（不考虑其他因素），请判断小宇是否能在 $12:00$前回到家，并说明理由．

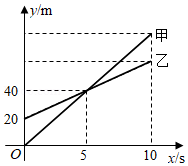
某日上午，甲，乙两车先后从 $A$地出发沿同一条公路匀速前往 $B$地，甲车8点出发，如图是其行驶路程 $s$（千米）随行驶时间 $t$（小时）变化的图象．乙车9点出发，若要在10点至11点之间（含10点和11点）追上甲车，则乙车的速度 $v$（单位：千米 $/$小时）的范围是　　．

暑假期间，小刚一家乘车去离家380公里的某景区旅游，他们离家的距离 $y\left(\mathit{km}\right)$与汽车行驶时间 $x\left(h\right)$之间的函数图象如图所示．

（1）从小刚家到该景区乘车一共用了多少时间？

（2）求线段 $\mathit{AB}$对应的函数解析式；

（3）小刚一家出发2.5小时时离目的地多远？

在一次机器"猫"抓机器"鼠"的展演测试中，"鼠"先从起点出发， $1\mathit{min}$ 后，"猫"从同一起点出发去追"鼠"，抓住"鼠"并稍作停留后，"猫"抓着"鼠"沿原路返回．"鼠"、"猫"距起点的距离 $y\left(m\right)$ 与时间 $x\left(\mathit{min}\right)$ 之间的关系如图所示．

（1）在"猫"追"鼠"的过程中，"猫"的平均速度与"鼠"的平均速度的差是 　　 $m/\mathit{min}$ ；

（2）求 $\mathit{AB}$ 的函数表达式；

（3）求"猫"从起点出发到返回至起点所用的时间．

在"新冠"疫情期间，全国人民"众志成城，同心抗疫"，某商家决定将一个月获得的利润全部捐赠给社区用于抗疫．已知商家购进一批产品，成本为10元 $/$ 件，拟采取线上和线下两种方式进行销售．调查发现，线下的月销量 $y$ （单位：件）与线下售价 $x$ （单位：元 $/$ 件， $12⩽x<24)$ 满足一次函数的关系，部分数据如下表：

$x$ （元     $/$ 件）	12	13	14	15	16
$y$ （件     $)$	1200	1100	1000	900	800

（1）求 $y$ 与 $x$ 的函数关系式；

（2）若线上售价始终比线下每件便宜2元，且线上的月销量固定为400件．试问：当 $x$ 为多少时，线上和线下月利润总和达到最大？并求出此时的最大利润．

“五 $\cdot$一”期间，小明一家乘坐高铁前往某市旅游，计划第二天租用新能源汽车自驾出游．

根据以下信息，解答下列问题：

（1）设租车时间为 $x$小时，租用甲公司的车所需费用为 $y_1$元，租用乙公司的车所需费用为 $y_2$元，分别求出 $y_1$， $y_2$关于 $x$的函数表达式；

（2）请你帮助小明计算并选择哪个出游方案合算．

甲无人机从地面起飞，乙无人机从距离地面 $20m$ 高的楼顶起飞，两架无人机同时匀速上升 $10s$ ．甲、乙两架无人机所在的位置距离地面的高度 $y$ （单位： $m)$ 与无人机上升的时间 $x$ （单位： $s)$ 之间的关系如图所示．下列说法正确的是 $($ 　　 $)$

A．	$5s$ 时，两架无人机都上升了 $40m$
B．	$10s$ 时，两架无人机的高度差为 $20m$
C．	乙无人机上升的速度为 $8m/s$
D．	$10s$ 时，甲无人机距离地面的高度是 $60m$

某通讯公司就手机流量套餐推出三种方案，如下表：

	$A$ 方案	$B$ 方案	$C$ 方案
每月基本费用（元     $)$	20	56	266
每月免费使用流量（兆     $)$	1024	$m$	无限
超出后每兆收费（元     $)$	$n$	$n$

$A$ ， $B$ ， $C$ 三种方案每月所需的费用 $y$ （元 $)$ 与每月使用的流量 $x$ （兆 $)$ 之间的函数关系如图所示．

（1）请写出 $m$ ， $n$ 的值．

（2）在 $A$ 方案中，当每月使用的流量不少于1024兆时，求每月所需的费用 $y$ （元 $)$ 与每月使用的流量 $x$ （兆 $)$ 之间的函数关系式．

（3）在这三种方案中，当每月使用的流量超过多少兆时，选择 $C$ 方案最划算？

某品牌鞋子的长度 $\mathit{ycm}$ 与鞋子的"码"数 $x$ 之间满足一次函数关系．若22码鞋子的长度为 $16\mathit{cm}$ ，44码鞋子的长度为 $27\mathit{cm}$ ，则38码鞋子的长度为 $($ 　　 $)$

A．

$23\mathit{cm}$

B．

$24\mathit{cm}$

C．

$25\mathit{cm}$

D．

$26\mathit{cm}$

下面图片是七年级教科书中“实际问题与一元一次方程”的探究3．

探究3

电话计费问题

下表中有两种移动电话计费方式．

	月使用费 $/$元	主叫限定时间 $/\mathit{min}$	主叫超时费 $/$（元 $/\mathit{min})$	被叫
方式一	58	150	0.25	免费
方式二	88	350	0.19	免费

考虑下列问题：

月使用费固定收： 主叫不超限定时间不再收费，主叫超时部分加收超时费，被叫免费．

（1）设一个月内用移动电话主叫为 $\mathit{tmin}(t$是正整数）．根据上表，列表说明：当 $t$在不同时间范围内取值时，按方式一和方式二如何计费．

（2）观察你的列表，你能从中发现如何根据主叫时间选择省钱的计费方式吗？通过计算验证你的看法．

小明升入初三再看这个问题，发现两种计费方式，每一种都是因主叫时间的变化而引起计费的变化，他把主叫时间视为在正实数范围内变化，决定用函数来解决这个问题．

（1）根据函数的概念，小明首先将问题中的两个变量分别设为自变量 $x$和自变量的函数 $y$，请你帮小明写出：

$x$表示问题中的 　　， $y$表示问题中的 　　．

并写出计费方式一和二分别对应的函数解析式；

（2）在给出的正方形网格纸上画出（1）中两个函数的大致图象，并依据图象写出如何根据主叫时间选择省钱的计费方式．（注 $:$坐标轴单位长度可根据需要自己确定）

暑期将至，某健身俱乐部面向学生推出暑期优惠活动，活动方案如下．

方案一：购买一张学生暑期专享卡，每次健身费用按六折优惠；

方案二：不购买学生暑期专享卡，每次健身费用按八折优惠．

设某学生暑期健身 $x$（次 $)$，按照方案一所需费用为 $y_1$（元 $)$，且 $y_1=k_{1}x+b$；按照方案二所需费用为 $y_2$（元 $)$，且 $y_2=k_{2}x$．其函数图象如图所示．

（1）求 $k_1$和 $b$的值，并说明它们的实际意义；

（2）求打折前的每次健身费用和 $k_2$的值；

（3）八年级学生小华计划暑期前往该俱乐部健身8次，应选择哪种方案所需费用更少？说明理由．

为了美化环境，建设宜居成都，我市准备在一个广场上种植甲、乙两种花卉，经市场调查，甲种花卉的种植费用 $y$（元 $)$与种植面积 $x\left(m^2\right)$之间的函数关系如图所示，乙种花卉的种植费用为每平方米100元．

（1）直接写出当 $0⩽x⩽300$和 $x>300$时， $y$与 $x$的函数关系式；

（2）广场上甲、乙两种花卉的种植面积共 $1200m^2$，若甲种花卉的种植面积不少于 $200m^2$，且不超过乙种花卉种植面积的2倍，那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少？最少总费用为多少元？