如图,在平面直角坐标系中,点 是直线 上的动点,过点 作 轴,交直线 于点 ,当 时,设点 的横坐标为 ,则 的取值范围为 .

设一次函数 , 是常数, 的图象过 , 两点.
(1)求该一次函数的表达式;
(2)若点 在该一次函数图象上,求 的值.
(3)已知点 , 和点 , 在该一次函数图象上,设 ,判断反比例函数 的图象所在的象限,说明理由.
如图,直线 与 轴、 轴分别交于点 和点 ,点 、 分别为线段 、 的中点,点 为 上一动点,当 最小时,点 的坐标为

A. B. C. , D. ,
如图,在平面直角坐标系中,直线 与x轴、y轴分别交于A、B两点,点C在第二象限,若 ,则点C的坐标为 .

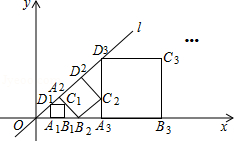
如图,点 在直线 上,过点 作 轴交直线 于点 ,以点 为直角顶点, 为直角边在 的右侧作等腰直角△ ,再过点 作 轴,分别交直线 和 于 , 两点,以点 为直角顶点, 为直角边在 的右侧作等腰直角△ ,按此规律进行下去,则等腰直角△ 的面积为 .(用含正整数 的代数式表示)

在平面直角坐标系中,一次函数 , 都是常数,且 的图象经过点 和 .
(1)当 时,求 的取值范围;
(2)已知点 在该函数的图象上,且 ,求点 的坐标.
如图,在平面直角坐标系中有直线 与双曲线 在直线上取点 ,过点 作 轴的垂线交双曲线于点 ,过 作 轴的垂线交直线于点 ,过点 作 轴的垂线交双曲线于点 ,过 作 轴的垂线交双曲线于点 过 作 轴的垂线交直线于点 , ,按此规律继续操作下去,依次得到直线上的点 , , , ,记点 的横坐标为 ,若 ,则 .

如图,点 在直线 上,过点 分别作 轴、 轴的平行线交直线 于点 , ,过点 作 轴的平行线交直线 于点 ,过点 作 轴的平行线交直线 于点 , ,按照此规律进行下去,则点 的横坐标为 .

在直角坐标系中,点 , 在同一个正比例函数图象上的是
A. , B. ,
C. , D. ,
若二次函数 的图象如图所示,则一次函数 与反比例函数 在同一个坐标系内的大致图象为

| A. |
|
B. |
|
| C. |
|
D. |
|
如图,在平面直角坐标系中,直线 为正比例函数 的图象,点 的坐标为 ,过点 作 轴的垂线交直线 于点 ,以 为边作正方形 ;过点 作直线 的垂线,垂足为 ,交 轴于点 ,以 为边作正方形 ;过点 作 轴的垂线,垂足为 ,交直线 于点 ,以 为边作正方形 , ,按此规律操作下所得到的正方形 的面积是 .