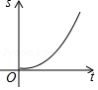
如图1, 的直径 厘米,点 在 上,设 的度数为 (单位:度, ,优弧 的弧长与劣弧 的弧长的差设为 (单位:厘米),图2表示 与 的函数关系,则 度.

如图,边长都为4的正方形 和正三角形 如图放置, 与 在一条直线上,点 与点 重合.现将 沿 方向以每秒1个单位的速度匀速运动,当点 与 重合时停止.在这个运动过程中,正方形 和 重叠部分的面积 与运动时间 的函数图象大致是

| A. |
|
B. |
|
C. |
|
D. |
|
如图, 、 、 、 为圆 的四等分点,动点 从圆心 出发,沿 的路线做匀速运动,当点 运动到圆心 时立即停止,设运动时间为 , 的度数为 度,则下列图象中表示 (度 与 之间的函数关系最恰当的是
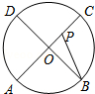
A.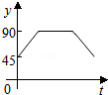 B.
B.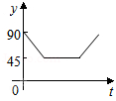
C.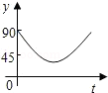 D.
D.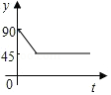
如图1,点从菱形
的顶点
出发,沿
以
的速度匀速运动到点
,图2是点
运动时,
的面积
随时间
变化的关系图象,则
的值为
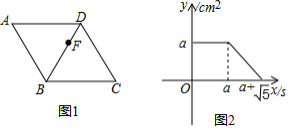
A.B.2C.
D.
如图,四边形 是矩形, , ,点 在对角线 上(不与点 , 重合), , 过点 , 交 于点 ,交 于点 , 交 于点 ,交 于点 , 交 于点 .设 , ,则 关于 的函数图象是

A. B.
B.
C. D.
D.
如图,菱形 的边长为 , ,点 从点 出发,以 的速度沿折线 运动,到达点 停止;点 同时从点 出发,以 的速度沿 运动,到达点 停止.设点 运动 时, 的面积为 ,则能够反映 与 之间函数关系的图象是

| A. |
|
B. |
|
| C. |
|
D. |
|
如图,点 的坐标为 ,点 是 轴正半轴上的一动点,以 为边作 ,使 , ,设点 的横坐标为 ,点 的纵坐标为 ,能表示 与 的函数关系的图象大致是
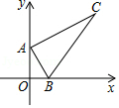
A.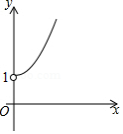 B.
B.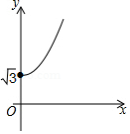
C.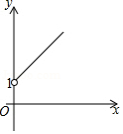 D.
D.
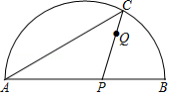
如图,是
与弦
所围成的图形的内部的一定点,
是弦
上一动点,连接
并延长交
于点
,连接
.已知
,设
,
两点间的距离为
,
,
两点间的距离为
,
,
两点间的距离为
.
小腾根据学习函数的经验,分别对函数,
随自变量
的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量的值进行取点、画图、测量,分别得到了
,
与
的几组对应值;
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
5.62 |
4.67 |
3.76 |
|
2.65 |
3.18 |
4.37 |
|
5.62 |
5.59 |
5.53 |
5.42 |
5.19 |
4.73 |
4.11 |
(2)在同一平面直角坐标系中,描出补全后的表中各组数值所对应的点
,
,并画出函数
,
的图象;

(3)结合函数图象,解决问题:当为等腰三角形时,
的长度约为
.
如图,正方形 的对角线 , 相交于点 ,点 在 上由点 向点 运动(点 不与点 重合),连接 ,将线段 绕点 逆时针旋转 得到线段 ,连接 交 于点 .设 的长为 , 的长为 ,下列图象中大致反映 与 之间的函数关系的是

A. B.
B.
C. D.
D.
如图,在矩形 中, , .点 从点 出发,以 的速度在矩形的边上沿 运动,点 与点 重合时停止运动.设运动的时间为 (单位: , 的面积为 (单位: ,则 随 变化的函数图象大致为

| A. |
|
B. |
|
| C. |
|
D. |
|
如图, 为矩形 的对角线,已知 , ,点 沿折线 以每秒1个单位长度的速度运动(运动到 点停止),过点 作 于点 ,则 的面积 与点 运动的路程 间的函数图象大致是

| A. |
|
B. |
|
| C. |
|
D. |
|
如图1,点 从 的顶点 出发,沿 匀速运动到点 ,图2是点 运动时,线段 的长度 随时间 变化的关系图象,其中 是曲线部分的最低点,则 的面积是
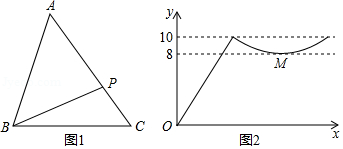
A.12B.24C.36D.48
如图1,点 从 的顶点 出发,沿 匀速运动到点 ,图2是点 运动时,线段 的长度 随时间 变化的关系图象,其中 为曲线部分的最低点,则 的面积是 .
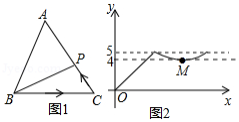
如图, ,点 从 点出发,以 的速度沿 的角平分线向右运动,在运动过程中,以 为圆心的圆始终保持与 的两边相切,设 的面积为 ,则 的面积 与圆心 运动的时间 的函数图象大致为
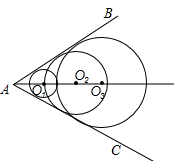
A.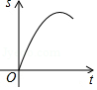 B.
B.
C. D.
D.