如图,在矩形 中, , .点 从点 出发,以 的速度在矩形的边上沿 运动,点 与点 重合时停止运动.设运动的时间为 (单位: , 的面积为 (单位: ,则 随 变化的函数图象大致为

| A. |
|
B. |
|
| C. |
|
D. |
|
如图,在矩形 中, , ,动点 , 同时从点 出发,点 沿 的路径运动,点 沿 的路径运动,点 , 的运动速度相同,当点 到达点 时,点 也随之停止运动,连接 .设点 的运动路程为 , 为 ,则 关于 的函数图象大致是

| A. |
|
B. |
|
| C. |
|
D. |
|
如图, 为矩形 的对角线,已知 , ,点 沿折线 以每秒1个单位长度的速度运动(运动到 点停止),过点 作 于点 ,则 的面积 与点 运动的路程 间的函数图象大致是

| A. |
|
B. |
|
| C. |
|
D. |
|
如图1,矩形 中,点 为 的中点,点 沿 从点 运动到点 ,设 , 两点间的距离为 , ,图2是点 运动时 随 变化的关系图象,则 的长为
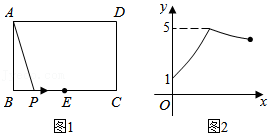
| A. |
4 |
B. |
5 |
C. |
6 |
D. |
7 |
图(1),在 中, ,点 从点 出发,沿三角形的边以 秒的速度逆时针运动一周,图(2)是点 运动时,线段 的长度 随运动时间 (秒 变化的关系图象,则图(2)中 点的坐标是

| A. |
|
B. |
|
C. |
|
D. |
|
如图1,在 中, , , ,点D为AB的中点,线段 上有一动点E,连接DE,作DA关于直线DE的对称图形,得到 ,过点F作 于点G.设A、E两点间的距离为 , 两点间的距离为
小军根据学习函数的经验,对因变量y随自变量x的变化而变化的规律进行了探究.
下面是小军的探究过程,请补充完整.

(1)列表:如表的已知数据是根据A,E两点间的距离x进行取点、画图、测量,分别得到了x与y的几组对应值:
x/cm |
0 |
0.51 |
1.03 |
1.41 |
1.50 |
1.75 |
2.20 |
2.68 |
3.00 |
3.61 |
4.10 |
4.74 |
5.00 |
y/cm |
0 |
0.94 |
1.91 |
2.49 |
|
2.84 |
3.00 |
2.84 |
2.60 |
2.00 |
1.50 |
0.90 |
0.68 |
请你通过计算补全表格;
(2)描点、连线:在平面直角坐标系 中(如图2),描出表中各组数值所对应的点 ,并画出y关于x的图象;
(3)探究性质:随着x值的不断增大,y的值是怎样变化的? ;
(4)解决问题:当 时,FG的长度大约是 cm(保留两位小数).
如图1,点 从 的顶点 出发,沿 匀速运动到点 ,图2是点 运动时,线段 的长度 随时间 变化的关系图象,其中 是曲线部分的最低点,则 的面积是
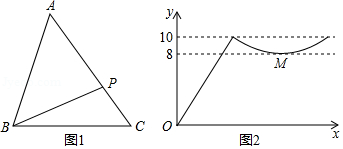
A.12B.24C.36D.48
如图1,点 从 的顶点 出发,沿 匀速运动到点 ,图2是点 运动时线段 的长度 随时间 变化的关系图象,其中点 为曲线部分的最低点,则 的边 的长度为

A.12B.8C.10D.13
如图1,小球从左侧的斜坡滚下,到达底端后又沿着右侧斜坡向上滚,在这个过程中,小球的运动速度 (单位: 与运动时间 (单位: 的函数图象如图2,则该小球的运动路程 (单位: 与运动时间 (单位: 之间的函数图象大致是

A. B.
B.
C. D.
D.
如图, 和 都是边长为2的等边三角形,它们的边 , 在同一条直线 上,点 , 重合.现将 沿着直线 向右移动,直至点 与 重合时停止移动.在此过程中,设点 移动的距离为 ,两个三角形重叠部分的面积为 ,则 随 变化的函数图象大致为
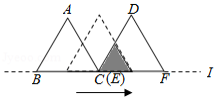
A.
B.
C.
D.
小亮在学习中遇到这样一个问题:
如图,点 是 上一动点,线段 ,点 是线段 的中点,过点 作 ,交 的延长线于点 .当 为等腰三角形时,求线段 的长度.
小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题.请将下面的探究过程补充完整:
(1)根据点 在 上的不同位置,画出相应的图形,测量线段 , , 的长度,得到下表的几组对应值.
|
0 |
1.0 |
2.0 |
3.0 |
4.0 |
5.0 |
6.0 |
7.0 |
8.0 |
|
8.0 |
7.7 |
7.2 |
6.6 |
5.9 |
|
3.9 |
2.4 |
0 |
|
8.0 |
7.4 |
6.9 |
6.5 |
6.1 |
6.0 |
6.2 |
6.7 |
8.0 |
操作中发现:
①“当点 为 的中点时, ”.则上表中 的值是 5.0 ;
②“线段 的长度无需测量即可得到”.请简要说明理由.
(2)将线段 的长度作为自变量 , 和 的长度都是 的函数,分别记为 和 ,并在平面直角坐标系 中画出了函数 的图象,如图所示.请在同一坐标系中画出函数 的图象;
(3)继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当 为等腰三角形时,线段 长度的近似值(结果保留一位小数).


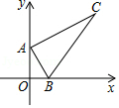
如图,点 的坐标为 ,点 是 轴正半轴上的一动点,以 为边作 ,使 , ,设点 的横坐标为 ,点 的纵坐标为 ,能表示 与 的函数关系的图象大致是
A.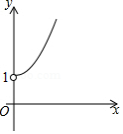 B.
B.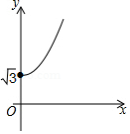
C.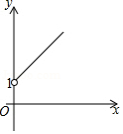 D.
D.
已知点 为某个封闭图形边界上一定点,动点 从点 出发,沿其边界顺时针匀速运动一周,设点 的运动时间为 ,线段 的长度为 ,表示 与 的函数图象大致如图所示,则该封闭图形可能是
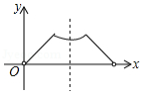
A.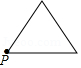 B.
B.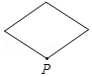
C.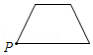 D.
D.
如图1, 为矩形 的边 上一点,点 从点 出发沿折线 运动到点 停止,点 从点 出发沿 运动到点 停止,它们运动的速度都是 .若点 、点 同时开始运动,设运动时间为 , 的面积为 ,已知 与 之间的函数图象如图2所示.
给出下列结论:①当 时, 是等腰三角形;② ;③当 时, ;④在运动过程中,使得 是等腰三角形的 点一共有3个;⑤ 与 相似时, .
其中正确结论的序号是 .
