如图,点 P在直线 AB上方,且∠ APB=90°, PC⊥ AB于 C,若线段 AB=6, AC= x, S △ PAB= y,则 y与 x的函数关系图象大致是( )

| A. |
|
B. |
|
| C. |
|
D. |
|
如图1,正△ ABC的边长为4,点 P为 BC边上的任意一点,且∠ APD=60°, PD交 AC于点 D,设线段 PB的长度为 x,图1中某线段的长度为 y, y与 x的函数关系的大致图象如图2,则这条线段可能是图1中的( )

| A. |
线段AD |
B. |
线段AP |
C. |
线段PD |
D. |
线段CD |
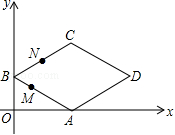
如图,在平面直角坐标系中,四边形 ABCD是菱形,点 B的坐标是(0,4),点 D的坐标 是(8 ,4),点 M和点 N是两个动点,其中点 M从点 B出发,沿 BA以每秒2个单位长度的速度做匀速运动,到点 A后停止,同时点 N从点 B出发,沿折线 BC→ CD以每秒4个单位长度的速度做匀速运动,如果其中一个点停止运动,则另一点也停止运动,设 M, N两点的运动时间为 x,△ BMN的面积为 y,下列图象中能表示 y与 x的函数关系的图象大致是( )
| A. |
|
B. |
|
| C. |
|
D. |
|
如图,边长为2的等边△ABC和边长为1的等边△A′B′C′,它们的边B′C′,BC位于同一条直线l上,开始时,点C′与B重合,△ABC固定不动,然后把△A′B′C′自左向右沿直线l平移,移出△ABC外(点B′与C重合)停止,设△A′B′C′平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( )

A. B.
B.
C. D.
D.
如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
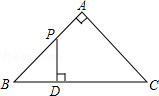
A.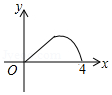 B.
B.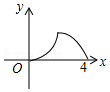
C.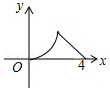 D.
D.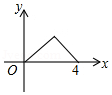
如图,△ABC中,AB=6,BC=8, ,点D是边BC上的一个动点(点D与点B不重合),过点D作DE⊥AB,垂足为E,点F是AD的中点,连接EF,设△AEF的面积为y,点D从点B沿BC运动到点C的过程中,D与B的距离为x,则能表示y与x的函数关系的图象大致是( )

A.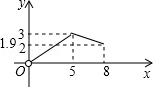 B.
B.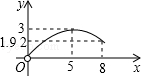
C. D.
D.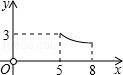
如图,在正方形 ABCD中,点 P从点 A出发,沿着正方形的边顺时针方向运动一周,则△ APC的面积 y与点 P运动的路程 x之间形成的函数关系图象大致是( )

| A. |
|
B. |
|
| C. |
|
D. |
|
如图,在菱形 中, , .动点 从点 出发,以每秒1个单位长度的速度沿折线 运动到点 ,同时动点 从点 出发,以相同速度沿折线 运动到点 ,当一个点停止运动时,另一点也随之停止.设 的面积为 ,运动时间为 秒.则下列图象能大致反映 与 之间函数关系的是

| A. |
|
B. |
|
| C. |
|
D. |
|
如图①,在 中, , ,点 是边 的中点,点 是边 上一动点,设 , .图②是 关于 的函数图象,其中 是图象上的最低点.那么 的值为 .

如图,在菱形 中, , .动点 从点 出发,以每秒1个单位长度的速度沿折线 运动到点 ,同时动点 从点 出发,以相同速度沿折线 运动到点 ,当一个点停止运动时,另一点也随之停止.设 的面积为 ,运动时间为 秒.则下列图象能大致反映 与 之间函数关系的是

| A. |
|
B. |
|
| C. |
|
D. |
|
如图,在四边形 中, , , , , .动点 , 同时从点 出发,点 以 的速度沿 向终点 运动,点 以 的速度沿折线 向终点 运动.设点 的运动时间为 , 的面积为 ,则下列图象能大致反映 与 之间函数关系的是

| A. |
|
B. |
|
| C. |
|
D. |
|
如图,在 中, , , 于点 .点 从点 出发,沿 的路径运动,运动到点 停止,过点 作 于点 ,作 于点 .设点 运动的路程为 ,四边形 的面积为 ,则能反映 与 之间函数关系的图象是

| A. |
|
B. |
|
| C. |
|
D. |
|
如图①, 为矩形 的边 上一点,点 从点 出发沿折线 运动到点 停止,点 从点 出发沿 运动到点 停止,它们的运动速度都是 .现 , 两点同时出发,设运动时间为 , 的面积为 ,若 与 的对应关系如图②所示,则矩形 的面积是

| A. |
|
B. |
|
C. |
|
D. |
|
如图1,在平面直角坐标系中, 在第一象限,且 轴.直线 从原点 出发沿 轴正方向平移,在平移过程中,直线被 截得的线段长度 与直线在 轴上平移的距离 的函数图象如图2所示.那么 的面积为

| A. |
3 |
B. |
|
C. |
6 |
D. |
|