李叔叔开车上班,最初以某一速度匀速行驶,中途停车加油耽误了几分钟,为了按时到单位,李叔叔在不违反交通规则的前提下加快了速度,仍保持匀速行驶,则汽车行驶的路程 (千米)与行驶的时间 (小时)的函数关系的大致图象是
| A. |
|
B. |
|
| C. |
|
D. |
|
周末,自行车骑行爱好者甲、乙两人相约沿同一路线从A地出发前往B地进行骑行训练,甲、乙分别以不同的速度匀速骑行,乙比甲早出发5分钟.乙骑行25分钟后,甲以原速的 继续骑行,经过一段时间,甲先到达B地,乙一直保持原速前往B地.在此过程中,甲、乙两人相距的路程y(单位:米)与乙骑行的时间x(单位:分钟)之间的关系如图所示,则乙比甲晚 分钟到达B地.

如图,是 市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是

A. B. C. D.
将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一个注水管沿大容器内壁匀速注水,如图所示,则小水杯内水面的高度 与注水时间 的函数图象大致为图中的

A. B.
B.
C. D.
D.
甲、乙两地相距 ,一辆汽车上午 从甲地出发驶往乙地,匀速行驶了一半的路程后将速度提高了 ,并继续匀速行驶至乙地,汽车行驶的路程 与时间 之间的函数关系如图所示,该车到达乙地的时间是当天上午

A. B. C. D.
如图,一个函数的图象由射线 、线段 、射线 组成,其中点 , , , ,则此函数
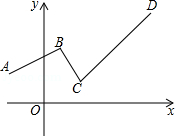
A.当 时, 随 的增大而增大B.当 时, 随 的增大而减小
C.当 时, 随 的增大而增大D.当 时, 随 的增大而减小
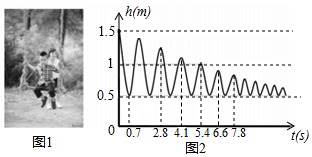
小红帮弟弟荡秋千(如图 ,秋千离地面的高度 与摆动时间 之间的关系如图2所示.
(1)根据函数的定义,请判断变量 是否为关于 的函数?
(2)结合图象回答:
①当 时, 的值是多少?并说明它的实际意义.
②秋千摆动第一个来回需多少时间?
在同一条道路上,甲车从 地到 地,乙车从 地到 地,乙先出发,图中的折线段表示甲、乙两车之间的距离 (千米)与行驶时间 (小时)的函数关系的图象,下列说法错误的是

A.乙先出发的时间为0.5小时
B.甲的速度是80千米 小时
C.甲出发0.5小时后两车相遇
D.甲到 地比乙到 地早 小时
均匀地向一个容器注水,最后把容器注满,在注水过程中,水面高度 随时间 的变化规律如图所示(图中 为折线),这个容器的形状可以是

A. B.
B.
C. D.
D.
如图,在 中, , , 是 上的一点(不与 、 重合), ,垂足是点 ,设 ,四边形 的周长为 ,则下列图象能大致反映 与 之间的函数关系的是

A.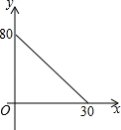 B.
B.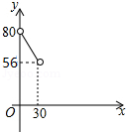
C.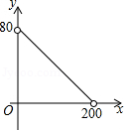 D.
D.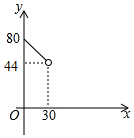
已知圆锥的侧面积是 ,若圆锥底面半径为 ,母线长为 ,则 关于 的函数图象大致是
A. B.
B.
C.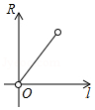 D.
D.
回顾初中阶段函数的学习过程,从函数解析式到函数图象,再利用函数图象研究函数的性质,这种研究方法主要体现的数学思想是
A.数形结合B.类比C.演绎D.公理化
如图,在物理课上,小明用弹簧秤将铁块 悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度,则下图能反映弹簧秤的读数 (单位: 与铁块被提起的高度 (单位: 之间的函数关系的大致图象是

A. B.
B.
C. D.
D.
小明和小华是同班同学,也是邻居,某日早晨,小明 先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公交汽车到了学校.如图是他们从家到学校已走的路程 (米 和所用时间 (分钟)的关系图.则下列说法中错误的是

A.小明吃早餐用时5分钟
B.小华到学校的平均速度是240米 分
C.小明跑步的平均速度是100米 分
D.小华到学校的时间是