规定: 表示不大于 的最大整数, 表示不小于 的最小整数, 表示最接近 的整数 , 为整数),例如: , , .则下列说法正确的是 .(写出所有正确说法的序号)
①当 时, ;
②当 时, ;
③方程 的解为 ;
④当 时,函数 的图象与正比例函数 的图象有两个交点.
下面哪幅图,可以大致刻画出苹果成熟后从树上下落过程中(落地前),速度变化的情况
A. B.
B.
C. D.
D.
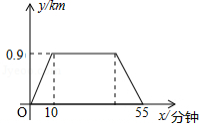
小明从家到图书馆看报然后返回,他离家的距离 与离家的时间 之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为 .
甲、乙两车从 地出发,匀速驶向 地.甲车以 的速度行驶 后,乙车才沿相同路线行驶.乙车先到达 地并停留 后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离 与乙车行驶时间 之间的函数关系如图所示.下列说法:①乙车的速度是 ;② ;③点 的坐标是 ;④ .其中说法正确的有

A.4个B.3个C.2个D.1个
“龟兔赛跑”这则寓言故事讲述的是比赛中兔子开始领先,但它因为骄傲在途中睡觉,而乌龟一直坚持爬行最终贏得比赛,下列函数图象可以体现这一故事过程的是
A.
B.
C.
D.
小明和哥哥从家里出发去买书,从家出发走了20分钟到一个离家1000米的书店.小明买了书后随即按原路返回;哥哥看了20分钟书后,用15分钟返家.下面的图象中哪一个表示哥哥离家时间与距离之间的关系
A.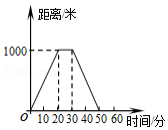
B.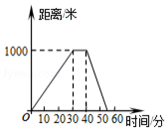
C.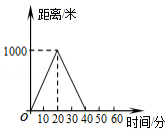
D.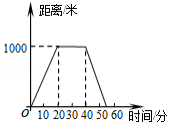
探究函数 与 的相关性质.
(1)小聪同学对函数 进行了如下列表、描点,请你帮他完成连线的步骤;观察图象可得它的最小值为 ,它的另一条性质为 ;
|
|
|
|
|
1 |
|
2 |
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
(2)请用配方法求函数 的最小值;
(3)猜想函数 的最小值为 .

随着时代的进步,人们对 (空气中直径小于等于2.5微米的颗粒)的关注日益密切.某市一天中 的值 随时间 的变化如图所示,设 表示0时到 时 的值的极差(即0时到 时 的最大值与最小值的差),则 与 的函数关系大致是

A. B.
B.
C. D.
D.
某周日上午 小宇从家出发,乘车1小时到达某活动中心参加实践活动. 时他在活动中心接到爸爸的电话,因急事要求他在 前回到家,他即刻按照来活动中心时的路线,以5千米 小时的平均速度快步返回.同时,爸爸从家沿同一路线开车接他,在距家20千米处接上了小宇,立即保持原来的车速原路返回.设小宇离家 (小时)后,到达离家 (千米)的地方,图中折线 表示 与 之间的函数关系.
(1)活动中心与小宇家相距 千米,小宇在活动中心活动时间为 小时,他从活动中心返家时,步行用了 小时;
(2)求线段 所表示的 (千米)与 (小时)之间的函数关系式(不必写出 所表示的范围);
(3)根据上述情况(不考虑其他因素),请判断小宇是否能在 前回到家,并说明理由.

小强的爸爸从家骑自行车去图书馆借书,途中遇到了从图书馆步行回家的小强,爸爸借完书后迅速回家,途中追上了小强,便用自行车载上小强一起回家,结果爸爸比自己单独骑车回家晚到1分钟,两人与家的距离 (千米)和爸爸从家出发后的时间 (分钟)之间的关系如图所示.
(1)图书馆离家有多少千米?
(2)爸爸和小强第一次相遇时,离家多少千米?
(3)爸爸载上小强后一起回家的速度是多少?

为了节能减排,鼓励居民节约用电,某市出台了新的居民用电收费标准:(1)若每户居民每月用电量不超过100度,则按0.60元 度计算;(2)若每户居民每月用电量超过100度,则超过部分按0.8元 度计算(未超过部分仍按每度电0.60元 度计算),现假设某户居民某月用电量是 (单位:度),电费为 (单位:元),则 与 的函数关系用图象表示正确的是
A. B.
B.
C. D.
D.
如图是自动测温仪记录的图象,它反映了齐齐哈尔市的春季某天气温 如何随时间 的变化而变化,下列从图象中得到的信息正确的是

A.0点时气温达到最低
B.最低气温是零下
C.0点到14点之间气温持续上升
D.最高气温是
均匀地向一个容器注水,最后将容器注满.在注水过程中,水的高度 随时间 的变化规律如图所示,这个容器的形状可能是
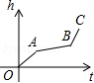
A. B.
B. C.
C. D.
D.