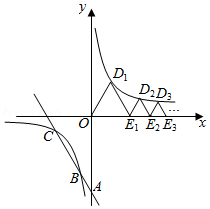
如图,在平面直角坐标系中,△ ,△ ,△ , 都是等腰直角三角形,其直角顶点 , , , 均在直线 上.设△ ,△ ,△ , 的面积分别为 , , , ,依据图形所反映的规律, .

如图,平面直角坐标系中, 经过三点 , , ,点 是 上的一动点.当点 到弦 的距离最大时, 的值是

A.2B.3C.4D.5
如图,平面直角坐标系 中,矩形 的边 、 分别落在 、 轴上,点 坐标为 ,反比例函数 的图象与 边交于点 ,与 边交于点 ,连接 ,将 沿 翻折至△ 处,点 恰好落在正比例函数 图象上,则 的值是

A. B. C. D.
如图,直线 与 轴交于点 ,与双曲线 在第三象限交于 、 两点,且 .下列等边三角形△ ,△ ,△ , 的边 , , , 在 轴上,顶点 , , , 在该双曲线第一象限的分支上,则 ,前25个等边三角形的周长之和为 .
如图,边长为4的正六边形 的中心与坐标原点 重合, 轴,将正六边形 绕原点 顺时针旋转 次,每次旋转 .当 时,顶点 的坐标为 .

已知 、 、 为常数,点 在第二象限,则关于 的方程 根的情况是
A.有两个相等的实数根B.有两个不相等的实数根
C.没有实数根D.无法判断
如图,在平面直角坐标系中, 的顶点坐标分别为 , , ,点 绕点 旋转 得到点 ,点 绕点 旋转 得到点 ,点 绕点 旋转 得到点 ,点 绕点 旋转 得到点 , ,按此作法进行下去,则点 的坐标为 .
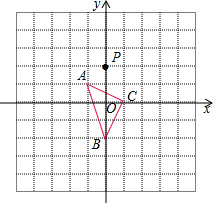
如图,在平面直角坐标系中, 的顶点坐标分别为 , , ,点 绕点 旋转 得到点 ,点 绕点 旋转 得到点 ,点 绕点 旋转 得到点 ,点 绕点 旋转 得到点 , ,按此作法进行下去,则点 的坐标为 .

如图,在平面直角坐标系中,点 ,直线 与 轴交于点 ,以 为边作等边 ,过点 作 轴,交直线 于点 ,以 为边作等边△ ,过点 作 轴,交直线 于点 ,以 为边作等边△ ,以此类推 ,则点 的纵坐标是 .

如图,菱形 的顶点 、 在 轴上 在 的左侧),顶点 、 在 轴上方,对角线 的长是 ,点 为 的中点,点 在菱形 的边上运动.当点 到 所在直线的距离取得最大值时,点 恰好落在 的中点处,则菱形 的边长等于

A. B. C. D.3
如图,将一等边三角形的三条边各8等分,按顺时针方向(图中箭头方向)标注各等分点的序号0、1、2、3、4、5、6、7、8,将不同边上的序号和为8的两点依次连接起来,这样就建立了“三角形”坐标系.在建立的“三角形”坐标系内,每一点的坐标用过这一点且平行(或重合)于原三角形三条边的直线与三边交点的序号来表示(水平方向开始,按顺时针方向),如点 的坐标可表示为 ,2, ,点 的坐标可表示为 ,1, ,按此方法,则点 的坐标可表示为 .
