温州某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件利润减少2元.设每天安排 人生产乙产品.
(1)根据信息填表:
产品种类 |
每天工人数(人 |
每天产量(件 |
每件产品可获利润(元 |
甲 |
|
|
15 |
乙 |
|
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润 (元 的最大值及相应的 值.
我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若 , ,则该矩形的面积为
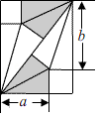
A.20B.24C. D.
欧几里得的《原本》记载,形如 的方程的图解法是:画 ,使 , , ,再在斜边 上截取 .则该方程的一个正根是

A. 的长B. 的长C. 的长D. 的长
根据衢州市统计局发布的统计数据显示,衢州市近5年国民生产总值数据如图1所示,2016年国民生产总值中第一产业,第二产业,第三产业所占比例如图2所示.

请根据图中信息,解答下列问题:
(1)求2016年第一产业生产总值(精确到1亿元)
(2)2016年比2015年的国民生产总值增加了百分之几?(精确到
(3)若要使2018年的国民生产总值达到1573亿元,求2016年至2018年我市国民生产总值的平均增长率(精确到
随着某市养老机构(养老机构指社会福利院、养老院、社区养老中心等)建设稳步推进,拥有的养老床位不断增加.
(1)该市的养老床位数从2013年底的2万个增长到2015年底的2.88万个,求该市这两年(从2013年度到2015年底)拥有的养老床位数的平均年增长率;
(2)若该市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共100间,这三类养老专用房间分别为单人间 个养老床位),双人间 个养老床位),三人间 个养老床位),因实际需要,单人间房间数在10至30之间(包括10和 ,且双人间的房间数是单人间的2倍,设规划建造单人间的房间数为 .
①若该养老中心建成后可提供养老床位200个,求 的值;
②求该养老中心建成后最多提供养老床位多少个?最少提供养老床位多少个?
某市从2017年开始大力发展“竹文化”旅游产业.据统计,该市2017年“竹文化”旅游收入约为2亿元.预计2019“竹文化”旅游收入达到2.88亿元,据此估计该市2018年、2019年“竹文化”旅游收入的年平均增长率约为
A. B. C. D.
在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为
A.9人B.10人C.11人D.12人
我市某楼盘准备以每平方 6000 元的均价对外销售, 由于国务院有关房地产的新政策出台后, 购房者持币观望, 为了加快资金周转, 房地产开发商对价格经过连续两次下调后, 决定以每平方 4860 元的均价开盘销售, 则平均每次下调的百分率是
A . B . C . D .
某烘焙店生产的蛋糕礼盒分为六个档次,第一档次(即最低档次)的产品每天生产76件,每件利润10元.调查表明:生产每提高一个档次的蛋糕产品,该产品每件利润增加2元.
(1)若生产的某批次蛋糕每件利润为14元,此批次蛋糕属第几档次产品;
(2)由于生产工序不同,蛋糕产品每提高一个档次,一天产量会减少4件.若生产的某档次产品一天的总利润为1080元,该烘焙店生产的是第几档次的产品?
某市创建“绿色发展模范城市”,针对境内长江段两种主要污染源:生活污水和沿江工厂污染物排放,分别用“生活污水集中处理”(下称甲方案)和“沿江工厂转型升级”(下称乙方案)进行治理,若江水污染指数记为 ,沿江工厂用乙方案进行一次性治理(当年完工),从当年开始,所治理的每家工厂一年降低的 值都以平均值 计算.第一年有40家工厂用乙方案治理,共使 值降低了12.经过三年治理,境内长江水质明显改善.
(1)求 的值;
(2)从第二年起,每年用乙方案新治理的工厂数量比上一年都增加相同的百分数 ,三年来用乙方案治理的工厂数量共190家,求 的值,并计算第二年用乙方案新治理的工厂数量;
(3)该市生活污水用甲方案治理,从第二年起,每年因此降低的 值比上一年都增加一个相同的数值 .在(2)的情况下,第二年,用乙方案所治理的工厂合计降低的 值与当年用甲方案治理降低的 值相等,第三年,用甲方案使 值降低了39.5.求第一年用甲方案治理降低的 值及 的值.
某市总预算 亿元用三年时间建成一条轨道交通线.轨道交通线由线路敷设、搬迁安置、辅助配套三项工程组成.从2015年开始,市政府在每年年初分别对三项工程进行不同数额的投资.
2015年年初,对线路敷设、搬迁安置的投资分别是辅助配套投资的2倍、4倍.随后两年,线路敷设投资每年都增加 亿元,预计线路敷设三年总投资为54亿元时会顺利如期完工;搬迁安置投资从2016年年初开始逐年按同一百分数递减,依此规律,在2017年年初只需投资5亿元,即可顺利如期完工;辅助配套工程在2016年年初的投资在前一年基础上的增长率是线路敷设2016年投资增长率的1.5倍,2017年年初的投资比该项工程前两年投资的总和还多4亿元,若这样,辅助配套工程也可以如期完工.经测算,这三年的线路敷设、辅助配套工程的总投资资金之比达到 .
(1)这三年用于辅助配套的投资将达到多少亿元?
(2)市政府2015年年初对三项工程的总投资是多少亿元?
(3)求搬迁安置投资逐年递减的百分数.
为满足社区居民健身的需要,市政府准备采购若干套健身器材免费提供给社区,经考察,劲松公司有 , 两种型号的健身器材可供选择.
(1)劲松公司2015年每套 型健身器材的售价为2.5万元,经过连续两年降价,2017年每套售价为1.6万元,求每套 型健身器材年平均下降率 ;
(2)2017年市政府经过招标,决定年内采购并安装劲松公司 , 两种型号的健身器材共80套,采购专项经费总计不超过112万元,采购合同规定:每套 型健身器材售价为1.6万元,每套 型健身器材售价为 万元.
① 型健身器材最多可购买多少套?
②安装完成后,若每套 型和 型健身器材一年的养护费分别是购买价的 和 ,市政府计划支出10万元进行养护,问该计划支出能否满足一年的养护需要?
受益于国家支持新能源汽车发展和“一带一路”发展战略等多重利好因素,我市某汽车零部件生产企业的利润逐年提高,据统计,2014年利润为2亿元,2016年利润为2.88亿元.
(1)求该企业从2014年到2016年利润的年平均增长率;
(2)若2017年保持前两年利润的年平均增长率不变,该企业2017年的利润能否超过3.4亿元?
某水果店在两周内,将标价为10元 斤的某种水果,经过两次降价后的价格为8.1元 斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第 天( 为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元 斤,设销售该水果第 (天)的利润为 (元),求 与 之间的函数关系式,并求出第几天时销售利润最大?
时间 (天) |
|
|
|
售价(元 斤) |
第1次降价后的价格 |
第2次降价后的价格 |
|
销量(斤) |
|
|
|
储存和损耗费用(元) |
|
|
|
(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?