初中数学一元二次方程解答题

2021年7月1日是建党100周年纪念日，在本月日历表上可以用一个方框圈出4个数（如图所示），若圈出的四个数中，最小数与最大数的乘积为65，求这个最小数（请用方程知识解答）．

关于 $x$ 的一元二次方程 $x^2+(2m+1)x+m^2-1=0$ 有两个不相等的实数根．

（1）求 $m$ 的取值范围；

（2）写出一个满足条件的 $m$ 的值，并求此时方程的根．

已知关于x的一元二次方程 $x^2﹣2x+m﹣1＝0$有两个实数根x₁，x₂．

（1）求m的取值范围；

（2）当时，求m的值．

阅读材料：用配方法求最值．已知x，y为非负实数，
∵
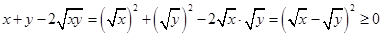
∴，当且仅当“x=y”时，等号成立．
示例：当x＞0时，求的最小值．
解：，当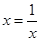，即x=1时，y的最小值为6．
（1）尝试：当x＞0时，求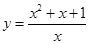的最小值．
（2）问题解决：随着人们生活水平的快速提高，小轿车已成为越来越多家庭的交通工具，假设某种小轿车的购车费用为10万元，每年应缴保险费等各类费用共计0．4万元，n年的保养、维护费用总和为万元．问这种小轿车使用多少年报废最合算（即：使用多少年的年平均费用最少，年平均费用=）？最少年平均费用为多少万元？

为积极响应新旧动能转换，提高公司经济效益，某科技公司近期研发出一种新型高科技设备，每台设备成本价为30万元，经过市场调研发现，每台售价为40万元时，年销售量为600台；每台售价为45万元时，年销售量为550台．假定该设备的年销售量 $y$（单位：台）和销售单价 $x$（单位：万元）成一次函数关系．

（1）求年销售量 $y$与销售单价 $x$的函数关系式；

（2）根据相关规定，此设备的销售单价不得高于70万元，如果该公司想获得10000万元的年利润，则该设备的销售单价应是多少万元？

请同学们认真阅读下面的一段文字材料，然后解答题目中提出的有关问题．
为解方程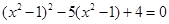，我们可以将视为一个整体，然后设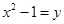，则原方程可化为 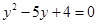①
解得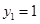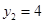，，当y=1时，，∴，；
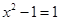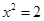当y=4时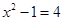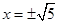，，∴，，∴原方程的解为=， =－，=，=－．
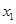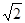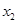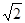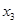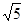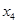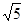解答问题：
（1）填空：在由原方程得到方程①的过程中，利用_________法达到了降次的目的，体现了_________的数学思想．
（2）解方程．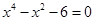

已知关于 x的一元二次方程 ax ²+ bx+ c＝0（ a≠0）有两个实数根 x ₁， x ₂，请用配方法探索有实数根的条件，并推导出求根公式，证明 x ₁• x ₂＝ $\frac{c}{a}$ ．

阅读材料：各类方程的解法

求解一元一次方程，根据等式的基本性质，把方程转化为 $x=a$的形式．求解二元一次方程组，把它转化为一元一次方程来解；类似的，求解三元一次方程组，把它转化为解二元一次方程组．求解一元二次方程，把它转化为两个一元一次方程来解．求解分式方程，把它转化为整式方程来解，由于“去分母”可能产生增根，所以解分式方程必须检验．各类方程的解法不尽相同，但是它们有一个共同的基本数学思想 $--$转化，把未知转化为已知．

用“转化”的数学思想，我们还可以解一些新的方程．例如，一元三次方程 $x^3+x^2-2x=0$，可以通过因式分解把它转化为 $x(x^2+x-2)=0$，解方程 $x=0$和 $x^2+x-2=0$，可得方程 $x^3+x^2-2x=0$的解．

（1）问题：方程 $x^3+x^2-2x=0$的解是 $x_1=0$， $x_2=$　　， $x_3=$　　；

（2）拓展：用“转化”思想求方程 $\sqrt{2x+3}=x$的解；

（3）应用：如图，已知矩形草坪 $\mathit{ABCD}$的长 $\mathit{AD}=8m$，宽 $\mathit{AB}=3m$，小华把一根长为 $10m$的绳子的一端固定在点 $B$，沿草坪边沿 $\mathit{BA}$， $\mathit{AD}$走到点 $P$处，把长绳 $\mathit{PB}$段拉直并固定在点 $P$，然后沿草坪边沿 $\mathit{PD}$、 $\mathit{DC}$走到点 $C$处，把长绳剩下的一段拉直，长绳的另一端恰好落在点 $C$．求 $\mathit{AP}$的长．

重庆小面是重庆美食的名片之一，深受外地游客和本地民众欢迎．某面馆向食客推出经典特色重庆小面，顾客可到店食用（简称"堂食"小面），也可购买搭配佐料的袋装生面（简称"生食"小面）．已知3份"堂食"小面和2份"生食"小面的总售价为31元，4份"堂食"小面和1份"生食"小面的总售价为33元．

（1）求每份"堂食"小面和"生食"小面的价格分别是多少元？

（2）该面馆在4月共卖出"堂食"小面4500份，"生食"小面2500份．为回馈广大食客，该面馆从5月1日起每份"堂食"小面的价格保持不变，每份"生食"小面的价格降低 $\frac{3}{4}a\%$ ．统计5月的销量和销售额发现："堂食"小面的销量与4月相同，"生食"小面的销量在4月的基础上增加 $\frac{5}{2}a\%$ ，这两种小面的总销售额在4月的基础上增加 $\frac{5}{11}a\%$ ．求 $a$ 的值．

小敏与小霞两位同学解方程 $3(x-3)={(x-3)}^2$的过程如下框：

小敏： 两边同除以 $(x-3)$，得 $3=x-3$， 则 $x=6$．

小霞： 移项，得 $3(x-3)-{(x-3)}^2=0$， 提取公因式，得 $(x-3)(3-x-3)=0$． 则 $x-3=0$或 $3-x-3=0$， 解得 $x_1=3$， $x_2=0$．

你认为他们的解法是否正确？若正确请在框内打“ $\surd$”；若错误请在框内打“ $\times$”，并写出你的解答过程．

已知关于 $x$的一元二次方程 $x^2+x-m=0$．

（1）若方程有两个不相等的实数根，求 $m$的取值范围；

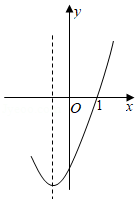
（2）二次函数 $y=x^2+x-m$的部分图象如图所示，求一元二次方程 $x^2+x-m=0$的解．

列方程（组 $)$解应用题

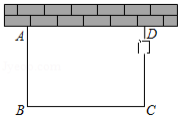
某驻村工作队，为带动群众增收致富，巩固脱贫攻坚成效，决定在该村山脚下，围一块面积为 $600m^2$的矩形试验茶园，便于成功后大面积推广．如图所示，茶园一面靠墙，墙长 $35m$，另外三面用 $69m$长的篱笆围成，其中一边开有一扇 $1m$宽的门（不包括篱笆）．求这个茶园的长和宽．

巴中市某楼盘准备以每平方米5000元的均价对外销售，由于有关部门关于房地产的新政策出台后，部分购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米4050元的均价开盘销售，若两次下调的百分率相同，求平均每次下调的百分率．

为响应国家全民阅读的号召，某社区鼓励居民到社区阅览室借阅读书，并统计每年的借阅人数和图书借阅总量（单位：本）．该阅览室在2014年图书借阅总量是7500本，2016年图书借阅总量是10800本．

（1）求该社区的图书借阅总量从2014年至2016年的年平均增长率；

（2）已知2016年该社区居民借阅图书人数有1350人，预计2017年达到1440人．如果2016年至2017年图书借阅总量的增长率不低于2014年至2016年的年平均增长率，那么2017年的人均借阅量比2016年增长 $a\%$，求 $a$的值至少是多少？

（1）计算：．

（2）为何值时，两个代数式，的值相等？