初中数学二元一次方程组的应用解答题

学校准备购进一批节能灯，已知1只 $A$ 型节能灯和3只 $B$ 型节能灯共需26元；3只 $A$ 型节能灯和2只 $B$ 型节能灯共需29元．

（1）求一只 $A$ 型节能灯和一只 $B$ 型节能灯的售价各是多少元；

（2）学校准备购进这两种型号的节能灯共50只，并且 $A$ 型节能灯的数量不多于 $B$ 型节能灯数量的3倍，请设计出最省钱的购买方案，并说明理由．

某景区售出的门票分为成人票和儿童票，购买3张成人票和1张儿童票共需350元，购买1张成人票和2张儿童票共需200元．

（1）求成人票和儿童票的单价；

（2）若干家庭结伴到该景区旅游，成人和儿童共30人．售票处规定：一次性购票数量达到30张，可购买团体票，每张票均按成人票价的八折出售，请你帮助他们选择花费最少的购票方式．

问题解决

糖葫芦一般是用竹签串上山楂，再蘸以冰糖制作而成．现将一些山楂分别串在若干根竹签上．如果每根竹签串5个山楂，还剩余4个山楂；如果每根竹签串8个山楂，还剩余7根竹签．这些竹签有多少根？山楂有多少个？

反思归纳

现有根竹签，个山楂．若每根竹签串个山楂，还剩余个山楂，则下列等式成立的是　　（填写序号）．

（1）；（2）；（3）．

被誉为“最美高铁”的长春至珲春城际铁路途经许多隧道和桥梁，其中隧道累计长度与桥梁累计长度之和为，隧道累计长度的2倍比桥梁累计长度多．求隧道累计长度与桥梁累计长度．

根据图中给出的信息，解答下列问题：

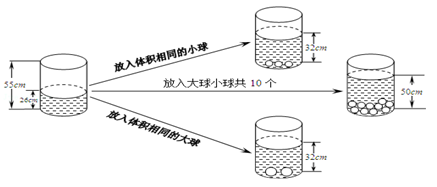
（1）放入一个小球水面升高      cm，放入一个大球水面升高      cm；
（2）如果要使水面上升到50cm，应放入大球、小球各多少个？

上个月，商店共卖出甲、乙两种商品1000件，这个月甲商品多卖出50%，乙商品少卖出10%，结果产品的总销量减少了4%，上个月甲、乙两种商品各卖出多少件？

（年青海省西宁市）兰新铁路的通车，圆了全国人民的一个梦，坐上火车去观赏青海门源百里油菜花海，感受大美青海独特的高原风光，暑假某校准备组织学生、老师到门源进行社会实践，为了便于管理，师生必须乘坐在同一列高铁上，根据报名人数，若都买一等座单程火车票需2340元，若都买二等座单程火车票花钱最少，则需1650元：

（1）参加社会实践的学生、老师各有多少人？
（2）由于各种原因，二等座火车票单程只能买x张（参加社会实践的学生人数＜x＜参加社会实践的总人数），其余的须买一等座火车票，在保证每位参与人员都有座位坐并且总费用最低的前提下，请你写出购买火车票的总费用（单程）y与x之间的函数关系式．

（年贵州省毕节）某商场有A，B两种商品，若买2件A商品和1件B商品，共需80元；若买3件A商品和2件B商品，共需135元．
（1）设A，B两种商品每件售价分别为a元、b元，求a、b的值；
（2）B商品每件的成本是20元，根据市场调查：若按（1）中求出的单价销售，该商场每天销售B商品100件；若销售单价每上涨1元，B商品每天的销售量就减少5件．
①求每天B商品的销售利润y（元）与销售单价（x）元之间的函数关系？
②求销售单价为多少元时，B商品每天的销售利润最大，最大利润是多少？

（年云南省曲靖市）某商场投入13800元资金购进甲、乙两种矿泉水共500箱，矿泉水的成本价和销售价如表所示：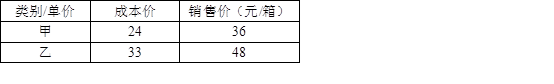

（1）该商场购进甲、乙两种矿泉水各多少箱？
（2）全部售完500箱矿泉水，该商场共获得利润多少元？

在“老年节”前夕，某公司工会组织323名退休职工到浙江杭州旅游，旅游前，工会确定每车保证有一名随团医生，并为此次旅游请了8名医生，现打算同时租甲、乙两种客车，其中甲种客车每辆载客50人，乙种客车每辆载客20人。
（1）请帮助工会设计租车方案。
（2）若甲种客车租金为800元/辆，乙种客车租金为600元/辆，工会按哪种方案租车最省钱？此时租金是多少？
（3）旅游前，一名医生由于有特殊情况，工会只能安排7名医生随团，为保证所租的每辆车安排有一名医生，租车方案调整为：同时租80座、50座和20座的大小三种客车，出发时，所租的三种客车的座位恰好坐满，请问工会的租车方案如何安排？

某学校为了绿化校园，决定从某苗圃购进甲、乙、丙三种树苗共80株，其中甲种树苗株树是乙种树苗株树的2倍，购买三种树苗的总金额不超过1320元，已知乙种树苗的单价是16元/株，乙种树苗的单价是甲种树苗的单价的，购买丙种树苗12株的金额等于购买甲种树苗20株的金额。
（1）甲、丙两种树苗的单价分别是多少元？
（2）若要求甲种树苗的株树不超过丙种树苗的株树，请你帮助设计共有哪些购买方案？