若关于 x, y的方程组 的解满足 x﹣ y>﹣ ,则 m的最小整数解为( )
| A. |
﹣3 |
B. |
﹣2 |
C. |
﹣1 |
D. |
0 |
某班为奖励在校运动会上取得好成绩的同学,花了200元钱购买甲、乙两种奖品共30件,其中甲种奖品每件8元,乙种奖品每件6元,则购买了甲种奖品 件.
甲、乙两人匀速在400米环形跑道上跑步,同时同地出发,如果相向而行,每隔1分钟相遇一次;如果同向而行,每隔5分钟相遇一次,已知甲比乙的速度快.设甲每分钟跑 x米,乙每分钟跑 y米,根据题意,列出方程组正确的是( )
| A. |
|
B. |
|
| C. |
|
D. |
|
某专卖店有 A, B两种商品.已知在打折前,买60件 A商品和30件 B商品用了1080元,买50件 A商品和10件 B商品用了840元; A, B两种商品打相同折以后,某人买500件 A商品和450件 B商品一共比不打折少花1960元,计算打了多少折?
某商场试销 A、 B两种型号的台灯,下表是两次进货情况统计:
| 进货情况 进货次数 |
进货数量(台) |
进货资金(元) |
|
| A |
B |
||
| 第一次 |
5 |
3 |
230 |
| 第二次 |
10 |
4 |
440 |
(1)求 A、 B两种型号台灯的进价各为多少元?
(2)经试销发现, A型号台灯售价 x(元)与销售数量 y(台)满足关系式2 x+ y=140,此商场决定两种型号台灯共进货100台,并一周内全部售出,若 B型号台灯售价定为20元,求 A型号台灯售价定为多少时,商场可获得最大利润?并通过计算说明商场获得最大利润时的进货方案.
某商场用39000元购进甲、乙两种商品,销售完后共获利6600元.其中甲种商品每件进价120元,售价138元;乙种商品每件进价100元,售价120元.
(1)该商场购进甲、乙两种商品各多少件?
(2)商场第二次以原进价购进甲、乙两种商品,购进乙种商品的件数不变,而购进甲种商品的件数是第一次的2倍,甲种商品按原价出售,而乙种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于8700元,乙种商品最低售价为多少元?
某商场用39000元购进甲、乙两种商品,销售完后共获利6600元.其中甲种商品每件进价120元,售价138元;乙种商品每件进价100元,售价120元.
(1)该商场购进甲、乙两种商品各多少件?
(2)商场第二次以原进价购进甲、乙两种商品,购进乙种商品的件数不变,而购进甲种商品的件数是第一次的2倍,甲种商品按原价出售,而乙种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于8700元,乙种商品最低售价为多少元?
七年级(2)班组织活动,班长李冰去商店购买笔记本和圆珠笔两种奖品,共花了12元,已知笔记本2元/本,圆珠笔1元/支,且每样东西至少买一件,则买到笔记本与圆珠笔数量相等的概率是 .
我市为全面推进"十个全覆盖"工作,绿化提质改造工程如火如荼地进行,某施工队计划购买甲、乙两种树苗共600棵对某标段道路进行绿化改造,已知甲种树苗每棵100元,乙种树苗每棵200元.
(1)若购买两种树苗的总金额为70000元,求需购买甲、乙两种树苗各多少棵?
(2)若购买甲种树苗的金额不少于购买乙种树苗的金额,至少应购买甲种树苗多少棵?
我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足.问鸡兔各几何.”其大意是:“有若干只鸡和兔关在同一笼子里,它们一共有35个头,94条腿.问笼中的鸡和兔各有多少只?”试用列方程(组 解应用题的方法求出问题的解.
解应用题的方法求出问题的解.
某校准备组织师生共60人,从南靖乘动车前往厦门参加夏令营活动,动车票价格如表所示:(教师按成人票价购买,学生按学生票价购买).
运行区间 |
成人票价(元 |
学生票价(元 |
||
出发站 |
终点站 |
一等座 |
二等座 |
二等座 |
南靖 |
厦门 |
26 |
22 |
16 |
若师生均购买二等座票,则共需1020元.
(1)参加活动的教师有 人,学生有 人;
(2)由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,而后续前往的教师和学生均购买二等座票.设提早前往的教师有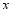 人,购买一、二等座票全部费用为
人,购买一、二等座票全部费用为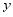 元.
元.
①求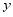 关于
关于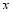 的函数关系式;
的函数关系式;
②若购买一、二等座票全部费用不多于1032元,则提早前往的教师最多只能多少人?