端午节前夕,某超市用1680元购进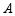 、
、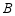 两种商品共60件,其中
两种商品共60件,其中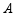 型商品每件24元,
型商品每件24元,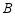 型商品每件36元.设购买
型商品每件36元.设购买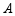 型商品
型商品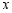 件、
件、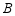 型商品
型商品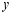 件,依题意列方程组正确的是
件,依题意列方程组正确的是
A.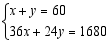 B.
B.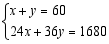
C.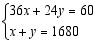 D.
D.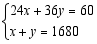
小明用计算器计算 的值,其按键顺序和计算器显示结果如表:

这时他才明白计算器是先做乘法再做加法的,于是他依次按键:

从而得到了正确结果,已知 是 的3倍,则正确的结果是
A.24B.39C.48D.96
某班有若干个活动小组,其中书法小组人数的3倍比绘画小组的人数多15人,绘画小组人数的2倍比书法小组的人数多5人,问:书法小组和绘画小组各有多少人?若设书法小组有 人,绘画小组有 人,那么可列方程组为
A. B.
C. D.
我国古代数学著作《增删算法统宗》记载"绳索量竿"问题:"一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托."其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长 尺,竿长 尺,则符合题意的方程组是
| A. |
|
B. |
|
| C. |
|
D. |
|
某校举行篮球赛,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.八年级一班在16场比赛中得26分.设该班胜 场,负 场,则根据题意,下列方程组中正确的是
| A. |
|
B. |
|
| C. |
|
D. |
|
在关于 、 的方程组 中,未知数满足 , ,那么 的取值范围在数轴上应表示为
A.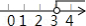 B.
B.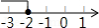
C. D.
D.
《九章算术》是中国古代数学著作之一,书中有这样的一个问题:五只雀,六只燕共重一斤,雀重燕轻,互换一只,恰好一样重.问:每只雀、燕的重量各为多少?设一只雀的重量为 斤,一只燕的重量为 斤,则可列方程组为
A. B.
C. D.
阅读理解: , , , 是实数,我们把符号 称为 阶行列式,并且规定: ,例如: .二元一次方程组 的解可以利用 阶行列式表示为: ;其中 , , .
问题:对于用上面的方法解二元一次方程组 时,下面说法错误的是
A. B.
C. D.方程组的解为
《九章算术》是中国传统数学的重要著作,书中有一道题"今有五雀六燕,集称之衡,雀俱重,燕俱轻;一雀一燕交而处,衡适平;并燕雀重一斤.问:燕雀一枚,各重几何?"译文:"五只雀、六只燕,共重1斤(古时1斤 两).雀重燕轻,互换其中一只,恰好一样重,问:每只雀、燕重量各为多少?"设雀重 两,燕重 两,可列出方程组
| A. |
|
B. |
|
| C. |
|
D. |
|
中国古代人民在生产生活中发现了许多数学问题,在《孙子算经》中记载了这样一个问题,大意为:有若干人乘车,若每车乘坐3人,则2辆车无人乘坐;若每车乘坐2人,则9人无车可乘,问共有多少辆车,多少人,设共有x辆车,y人,则可列方程组为( )
A. B.
C. D.