有一张边长为 厘米的正方形桌面,因为实际需要,需将正方形边长增加 厘米,木工师傅设计了如图所示的三种方案:
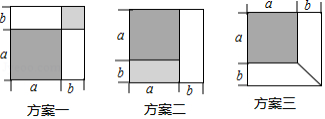
小明发现这三种方案都能验证公式: ,
对于方案一,小明是这样验证的:
请你根据方案二、方案三,写出公式的验证过程.
方案二:
方案三:
如图将4个长、宽分别均为a、b的长方形,摆成了一个大的正方形.利用面积的不同表示方法写出一个代数恒等式是 .

如图将4个长、宽分别均为 、
、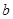 的长方形,摆成了一个大的正方形.利用面积的不同表示方法写出一个代数恒等式是__________________.
的长方形,摆成了一个大的正方形.利用面积的不同表示方法写出一个代数恒等式是__________________.
如图甲是一个长2m,宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图乙的形状拼成一个正方形.
(1)求图乙中阴影部分的面积.
(2)观察图乙,请你写出三个代数式 、
、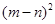 、
、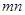 之间的等量关系式.
之间的等量关系式.
(3)根据(2)中的结论,若 ,
, ,求
,求 的值.
的值.
(4)有许多代数恒等式可以用图形的面积来表示.如图丙,它表示了 .
.
试画一个几何图形,使它的面积能表示: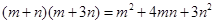 .
.
如图①是1个直角三角形和2个小正方形,直角三角形的三条边长分别是a、b、c,其中a、b是直角边.正方形的边长分别是a、b.

(1)将4个完全一样的直角三角形和2个小正方形构成一个大正方形(如图②).用两种不同的方法列代数式表示图②中的大正方形面积:
方法一: ; 方法二: ;
(2)观察图②,试写出 ,
,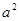 ,2ab,
,2ab, 这四个代数式之间的等量关系;
这四个代数式之间的等量关系;
(3)请利用(2)中等量关系解决问题:
已知图①中一个三角形面积是6,图②的大正方形面积是49,求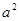 +
+ 的值.
的值.
(4)利用你发现的结论,求: 的值.
的值.
(1)在下列横线上用含有a,b的代数式表示相应图形的面积.
① ② ③ ④
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表示 ;
(3)利用(2)的结论计算9972+6×997+9的值.

如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.

(1)认为图②中的阴影部分的正方形的边长等于 .
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积,
方法① ;方法② .
(3)观察图②,你能写出(m+n)2,(m-n)2,4mn这三个代数式之间的等量关系吗?
(4)根据⑶题中的等量关系,解决如下问题:若a+b=6,ab=4,则求(a-b)2的值.
图1是一个长为2 ,宽为2
,宽为2 的长方形,沿图中虚线剪开,可分成四块小长方形.
的长方形,沿图中虚线剪开,可分成四块小长方形.

(1)求出图1的长方形面积;
(2)将四块小长方形拼成一个图2的正方形.利用阴影部分面积的不同表示方法,直接写出代数式( )2、(
)2、( )2、
)2、 之间的等量关系;
之间的等量关系;
(3)把四块小长方形不重叠地放在一个长方形的内部(如图3),未被覆盖的部分用阴影表示.求两块阴影部分的周长和(用含 、
、 的代数式表示).
的代数式表示).
图①是一个长为 、宽为
、宽为 的长方形,用这样四个全等的长方形,拼成如图②的正方形.
的长方形,用这样四个全等的长方形,拼成如图②的正方形.

(1)按要求填空:
ⅰ.请用含字母 、
、 的代数式表示图②中的阴影部分的正方形的边长: ;
的代数式表示图②中的阴影部分的正方形的边长: ;
ⅱ.请用含字母 、
、 的代数式,用两种不同的方法表示图②中阴影部分的面积:
的代数式,用两种不同的方法表示图②中阴影部分的面积:
方法1:
方法2:
ⅲ.观察图②,请写出代数式 、
、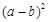 、
、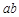 之间的等量关系: ;
之间的等量关系: ;
(2)根据(1)题中的等量关系,解决如下问题:
若 ,
, ,求
,求 的值.
的值.
阅读材料并回答问题:(本题8分)
我们知道,乘法公式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,如: ,就可以用图1或图2等图形的面积表示.
,就可以用图1或图2等图形的面积表示.
(1)请写出图3所表示的代数恒等式: ;
(2)试画一个几何图形,使它的面积表示: ;
;
(3)请仿照上述方法另写一个含有 ,
, 的代数恒等式,并画出与它对应的几何图形.
的代数恒等式,并画出与它对应的几何图形.