新学期，两摞规格相同的数学课本整齐的叠放在课桌上，请根据图中所给出的数据信息，解答下列问题：
（1）每本书的厚度为 cm，课桌的高度为 cm；
（2）当课本数为
（本）时，请直接写出同样叠放在桌面上的一摞数学课本高出地面的距离（用含的代数式表示）；
（3）利用（2）中的结论解决问题：桌面上有45本与题（1）中相同的数学课本，整齐叠放成一摞，若从中取走15本，求余下的数学课本高出地面的距离．
将一列有理数－1，2，－3，4，－5，6，……，如图所示有序排列．根据图中的排列规 律可知，“峰1”中峰顶的位置（C的位置）是有理数4，那么，“峰6”中C 的位置是有理数 ，2015应排在A、B、C、D、E中 的位置．
现有四个有理数3，4，－6，10，将这四个数（每个数用且只能用一次）进行加减乘除四则运算，使其运算的结果是24，请你写出一个符合条件的算式___________．
（1）若a与2b互为倒数，－c与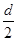
互为相反数，
，求
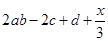的值．
（2）已知当x＝2时，代数式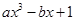
的值为－17，求当x＝－1时，代数式
的值是多少？
从2开始，连续的偶数相加，它们和的情况如下表：
（1）如果n=8时，那么S的值为________；
（2）由表中的规律猜想：用n的代数式表示S的公式为S=2+4+6+8+…+2n=_________；
（3）由上题的规律计算300+302+304+…+2010+2012的值（要有计算过程）．
在某次抗险救灾中，消防官兵的冲锋舟沿东西方向的河流营救灾民，早晨从A地出发，晚上到达B地，约定向东为正方向，当天的航行路程记录如下（单位：km）：＋14，－9，＋8，－7，＋13，－6，＋10，－5．
（1）通过计算说明：B地在A地的什么方向，与A地相距多远？
（2）救灾过程中，最远处离出发点A有多远？
（3）若冲锋舟每千米耗油0.5 L，油箱容量为29L，求途中还需补充多少升油．
将正方形图1作如下操作：第1次：分别连接各边中点如图2，得到5个正方形；第2次：将图2左上角正方形按上述方法再分割如图3，得到9个正方形…，以此类推，根据以上操作，若要得到2013个正方形，则需要操作的次数是（ ）
| A．502 | B．503 | C．504 | D．505 |
（本题10分）如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“和谐数”。如
，因此4，12，20这三个数都是和谐数。
（1）36和2016这两个数是和谐数吗？为什么？
（2）设两个连续偶数为2k+2和2k（其中k取非负整数），由这两个连续偶数构造的和谐数是4的倍数吗？为什么？
（3）介于1到200之间的所有“和谐数”之和为 ．
观察下列等式：
第1个等式：x1=
；
第2个等式：x2=
；
第3个等式：x3=
；
第4个等式：x4=
；
则xl+x2+x3+…+x10= ．
（本题9分）我们都知道无限不循环小数是无理数，而无限循环小数是可以化成分数的。例如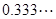
（3为循环节）是可以化成分数的，方法如下：
令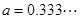
①
则
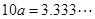②
②-①得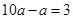
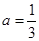
所以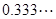可以化成分数为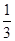
请你阅读上面材料完成下列问题：
（1）
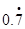化成分数是 ．
（2）请你将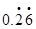 
化为分数．
（3）请你将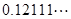
（即
）化为分数．
（本题9分）数轴上的点M对应的数是-4，一只甲虫从M点出发沿数轴以每秒2个单位长度的速度爬行，当它到达数轴上的N点后，立即返回到原点，共用11秒．
（1）甲虫爬行的路程是多少？
（2）点N对应的数是多少？
（3）点M和点N之间的距离是多少？
（本题8分）小明有5张写着不同数字的卡片，请你按要求抽出卡片，完成下列各问题：
（1）从中取出2张卡片，使这2张卡片上数字的乘积最小，乘积的最小值为 ；
（2）从中取出4张卡片，用学过的运算方法，使结果为24。写出运算式子。
（写出一种即可）算24的式子为 。
古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”，而把1、4、9、16 … 这样的数称为“正方形数”．从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是（ ）
| A．36=15+21 | B．49=18+31 | C．25="9+16" | D．13=3+10 |
，例如3*2＝
＝10，那么
*4＝______．
粤公网安备 44130202000953号