初中数学幂的乘方与积的乘方试题

观察下列等式：
12×231=132×21，
13×341=143×31，
23×352=253×32，
34×473=374×43，
62×286=682×26，
……
以上每个等式中两边数字是分别对称的，且每个等式中组成两位数与三位数的数字之间具有相同规律，我们称这类等式为“数字对称等式”．
（1）根据上述各式反映的规律填空，使式子成为“数字对称等式”：
①52×     ＝      ×25；
②      ×396＝693×     ．
（2）设这类等式左边两位数的十位数字为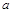，个位数字为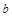，且2≤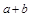≤9，写出表示“数字对称等式”一般规律的式子（含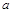、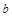），并说明理由．

读一读：
式子“1+2+3+4+5+…+100”表示从1开始的100个连续自然数的和．
由于上述式子比较长，书写也不方便，为了简便起见，我们可以将“1+2+3+4+5+…+100”表示为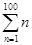，这里“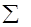”是求和符号．例如：“1+3+5+7+9+…+99”（即从1开始的100以内连续奇数的和）可表示为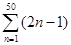；又如“1³+2³+3³+4³+5³+6³+7³+8³+9³+10³”可表示为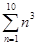． 同学们，通过对以上材料的阅读，请解答下列问题：
（1）“2+4+6+8+10+…+100”（即从2开始的100以内的连续偶数的和）用求和符号可表示为              ．
（2）计算: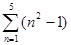的值

一辆货车从超市出发，向东走了2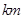到达小刚家，继续向东走了3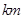到达小红家，又向西走了9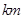到达小英家，最后回到超市．
（1）请以超市为原点，以向东方向为正方向，用1个单位长度表示1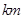，画出数轴，在数轴上表示出小刚家、小红家、小英家的位置；
（2）小英家距小刚家有多远？
（3）货车一共行驶了多少千米？

如图，数轴的单位长度为1．

（1）如果点B，D表示的数互为相反数，那么图中点A、点D表示的数分别是    、      ；
（2）当点B为原点时，在数轴上是否存在点M，使得点M到点A的距离是点M到点D的距离的2倍，若存在，请求出此时点M所表示的数；若不存在，说明理由；
（3） 在（2）的条件下，点A、点C分别以2个单位长度/秒和0.5个单位长度同时向右运动，同时点P从原点出发以3个单位长度/秒的速度向左运动，当点A与点C之间的距离为3个单位长度时，求点P所对应的数是多少？

（1）在下列横线上用含有a，b的代数式表示相应图形的面积．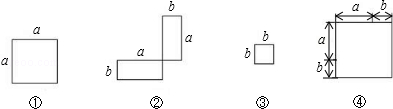

①__________②__________③__________④__________
（2）请在图④画出拼图并通过拼图，你发现前三个图形的面积与第四个图形面积之间有什么关系？请用数学式子表达：__________．
（3）利用（2）的结论计算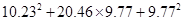的值．

已知：a与b是互为相反数，c与d互为倒数，m是绝对值最小的数，n是最大的负整数，则：
（1）a＋b＝       ，＝        ，m＝        ，n＝        ；
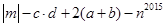（2）求：的值．

（本题12分）意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…，其中从第三个数起，每一个数都等于它前面两个数的和．现以这组数中的各个数作为正方形的边长值构造正方形：

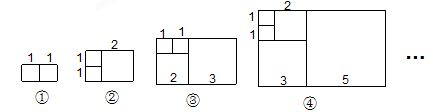
再分别依次从左到右取2个、3个、4个、5个…正方形拼成如下长方形并记为①、②、③、④、 …相应长方形的周长如下表所示：

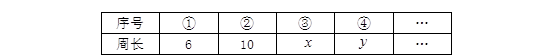
仔细观察图形，上表中的x=             ，y=            ．
若按此规律继续作长方形，则序号为⑧的长方形周长是               ．

在某次抗险救灾中，消防官兵的冲锋舟沿东西方向的河流抢救灾民，早晨从A地出发，晚上到达B 地，约定向东为正方向，当天的航行路程记录如下（单位：千米）：
+12，﹣9，+8，﹣7，+11，﹣6，+10，﹣5．
（1）B地在A地什么方向，距离A地多少千米？
（2）若冲锋舟每千米耗油0．5升，油箱容量为30升，求途中还需补充多少升油．

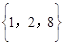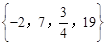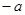把几个数用大括号括起来，中间用逗号断开，如：、，我们称之为集合，其中的数称其为集合的元素．如果一个集合满足：当有理数是集合的元素时，有理数10也必是这个集合的元素，这样的集合我们称为“好的集合”．例如集合｛10，0｝就是一个“好的集合”．
（1）集合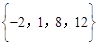        （填“是”或“不是”）“好的集合”．
（2）请你再写出两个好的集合（不得与上面出现过的集合重复）．
（3）在所有“好的集合”中，元素个数最少的集合是        ．

（本题4分）观察图形，解答问题：

（1）按下表已填写的形式填写表中的空格：

	图①	图②	图③
三个角上三个数的积	1×（－1）×2＝－2	（－3）×（－4）×（－5）＝－60
三个角上三个数的和	1＋（－1）＋2＝2	（－3）＋（－4）＋（－5）＝－12
积与和的商	（－2）÷2＝－1

 
（2）请用你发现的规律求出图④中的数x和图⑤中的数y．

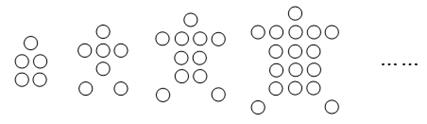
将一些相同的“○”按如图所示的规律依次摆放，观察每个“龟图”中的“○”的个数，则第10个“龟图”中的“○”的个数为          ．

观察下列一组数：1，2，2，3，3，3，4，4，4，4，5，5，5，5，5，6，…其中每个数n都连
续出现n次，那么这一组数的第119个数是            ．

如图，按此规律，第      行最后一个数是2017．

计算
（1）                
（2）
（3）           
（4）

2015年9月30日杭州西湖景区某公园人流量为7万，每张门票80元，“十一黄金周”景区迎来了旅游高峰期，游客从各个省市来到杭州，该公园统计：十一黄金周期间，游客人数与前一天相比，增加和减少的情况如下表：（记增加为正）．

日期	1号	2号	3号	4号	5号	6号	7号
人数（万人）	+5	-1．2	+5．7	-0．6	+1．8	-2．9	-2．5

 
（1）10月2号该公园的人流量是多少万人？
（2）“十一黄金周”期间，人流量最多和最少分别出现在哪一天？
（3）该公园的所有门票收入均要缴纳百分之五的税，求“十一黄金周”期间，该公园的实际收入．