初中数学整式的加减解答题

先化简，再求值：，其中．

A市、B市和C市分别有某种机器10台、10台、8台，现在决定把这些机器支援给D市18台，E市10台，已知调运机器的费用如下表所示：

	A市	B市	C市
D市	200元/台	300元/台	400元/台
E市	800元/台	700元/台	500元/台

设从A市、B市各调x台到D市，
（1）C市调运到D市的机器为___________台（用含x的代数式表示）；
（2）B市调运到E市的机器的费用为______________元（用含x的代数式表示，并化简）；
（3）求调运完毕后的总运费（用含x的代数式表示，并化简）；
（4）当x＝5和x＝8时，哪种调运方式总运费少？少多少？

（本小题满分6分）先化简，再求值．
，其中，．

有理数a、b、c在数轴上的位置如图：

（1）判断正负，用“＞”或“＜”填空：b－c    0，a＋b    0，c－a    0；
（2）化简：．

先化简，再求值：若A=，B=，其中，，求2A-B的值．

（1）先化简，再求值：，其中a＝－2，b＝3
（2）已知，ab＝－2，求代数式的值．

先化简，再求值：2（x²+2x﹣2）﹣（x²﹣2x﹣1），其中x=﹣．

在数的学习过程中，我们总会对其中一些具有某种特性的数进行研究，如学习自然数时，我们研究了偶数、奇数、合数、质数等．现在我们来研究一种特殊的自然数 “纯数”．

定义：对于自然数，在通过列竖式进行的运算时各位都不产生进位现象，则称这个自然数为“纯数”．

例如：32是“纯数”，因为在列竖式计算时各位都不产生进位现象；23不是“纯数”，因为在列竖式计算时个位产生了进位．

（1）请直接写出1949到2019之间的“纯数”；

（2）求出不大于100的“纯数”的个数，并说明理由．

有一电脑程序：每按一次按键，屏幕的 $A$ 区就会自动加上 $a^2$ ，同时 $B$ 区就会自动减去 $3a$ ，且均显示化简后的结果．已知 $A$ ， $B$ 两区初始显示的分别是25和 $-16$ ，如图．

如，第一次按键后， $A$ ， $B$ 两区分别显示：

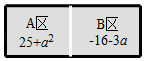
（1）从初始状态按2次后，分别求 $A$ ， $B$ 两区显示的结果；

（2）从初始状态按4次后，计算 $A$ ， $B$ 两区代数式的和，请判断这个和能为负数吗？说明理由．

先化简，再求值： $5(3a^{2}b-a{b}^2)-3(a{b}^2+5a^{2}b)$ ，其中 $a=\frac{1}{3}$ ， $b=-\frac{1}{2}$ ．

课堂上李老师把要化简求值的整式（7a²﹣6a²b+3a²b）﹣（﹣3a²﹣6a²b+3a²b+10a²﹣3）写完后，让王红同学任意给出一组a、b的值，老师自己说答案，当王红说完：“a=38，b=﹣32”后，李老师不假思索，立刻就说出答案“3”．同学们莫名其妙，觉得不可思议，但李老师用坚定的口吻说：“这个答案准确无误”，亲爱的同学你相信吗？请你通过计算说出其中的道理．

化简：
（1）2（2x-3y）-（3x+2y+1）；
（2）-（3a²-4ab）+[a²-2（2a+2ab）]．

有理数x、y在数轴上对应点如图所示：

（1）在数轴上表示、；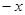
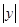（2）试把x、y、0、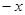、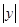这五个数从小到大用“＜”号连接；
（3）化简．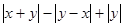

化简：
（1）；
（2）．

先化简，再求值：（x﹣2）（x+2）+x²（x﹣1），其中x=﹣1．