2015年初中毕业升学考试(湖北衡阳卷)数学
已知等腰三角形的两边长分别是5和6,则这个等腰三角形的周长为( ).
| A.11 | B.16 | C.17 | D.16或17 |
下列命题是真命题的是( ).
| A.对角线互相平分的四边形是平行四边形 |
| B.对角线相等的四边形是矩形 |
| C.对角线互相垂直的四边形是菱形 |
| D.对角线互相垂直平分的四边形是正方形 |
在今年“全国助残日”捐款活动中,某班级第一小组7名同学积极捐出自己的零花钱,奉献自己的爱心.他们捐款的数额分别是(单位:元)50,20,50,30,25,50,55,这组数据的众数和中位数分别是( ).
| A.50元,30元 | B.50元,40元 |
| C.50元,50元 | D.55元,50元 |
绿苑小区在规划设计时,准备在两幢楼房之间,设置一块面积为900平方米的矩形绿地,并且长比宽多10米.设绿地的宽为 米,根据题意,可列方程为( ).
米,根据题意,可列方程为( ).
A. |
B. |
C. |
D. |
如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔
顶端A的仰角为30°,再向电视塔方向前进100米到达F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( ).
A. |
B.51 | C. |
D.101 |
如图所示,小明为了测量学校里一池塘的宽度AB,选取可以直达A、B两点的点O 处,再分别取OA、OB的中点M、N,量得MN=20m,则池塘的宽度AB为 m.
如图,△ ,△
,△ ,△
,△ ,…,△
,…,△ ,都是等腰直角三角形.其中点
,都是等腰直角三角形.其中点 ,
, ,…,
,…, 在
在 轴上,点
轴上,点 ,
, ,…,
,…, ,在直线
,在直线 上.已知
上.已知 ,则
,则 的长为 .
的长为 .
(本小题满分6分)为了进一步了解义务教育阶段学生的体质健康状况,教育部对我市某中学九年级的部分学生进行了体质揣测.体质揣测的结果分为四个等级:优秀、良好、合格、不合格;根据调查结果绘制了下列两幅不完整的统计图,请你根据统计图提供的信息回答以下问题:

(1)在扇形统计图中,“合格“的百分比为 .
(2)本次体质抽测中,抽测结果为“不合格“等级的学生有 人.
(3)若该校九年级有400名学生,估计该校九年级体质为“不合格“等级的学生约有 人.
(本小题满分6分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(3,2)、B(3,5)、C(1,2).
(1)在平面直角坐标系中画出△ABC关于 轴对称的△A1B1C1;
轴对称的△A1B1C1;
(2)把△ABC绕点A顺时针旋转一定的角度,得图中的△AB2C2,点C2在AB上.
①旋转角为多少度?
②写出点B2的坐标.
(本小题满分6分)某校学生会正筹备一个“庆毕业”文艺汇演活动,现准备从4名(其中两男两女)节目主持候选人中,随机选取两人担任节目主持人,请用列表法或画树状图求选出的两名主持人“恰好为一男一女”的概率.
(本小题满分8分)某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体实验.测得成人服药后血液中药物深度 (微克/毫升)与服药时间
(微克/毫升)与服药时间 小时之间的函数关系如图所示(当
小时之间的函数关系如图所示(当 时,
时, 与
与 成反比).
成反比).
(1)根据图象分别求出血液中药物浓度上升和下降阶段 与
与 之间的函数关系式;
之间的函数关系式;
(2)问血液中药物浓度不低于4微克/毫升的持续时间为多少小时?
(本小题满分8分)如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.
(1)求证:CE为⊙O的切线;
(2)判断四边形AOCD是否为菱形?并说明理由.
(本小题满分10分)如图,顶点M在 轴上的抛物线与直线
轴上的抛物线与直线 相交于A、B两点,且点A在
相交于A、B两点,且点A在 轴上,点B的横坐标为2,连结AM、BM.
轴上,点B的横坐标为2,连结AM、BM.
(1)求抛物线的函数关系式;
(2)判断△ABM的形状,并说明理由;
(3)把抛物线与直线 的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(
的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为( ,
, ),当
),当 满足什么条件时,平移后的抛物线总有不动点?
满足什么条件时,平移后的抛物线总有不动点?
 的结果是( ).
的结果是( ).

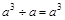

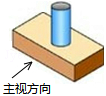


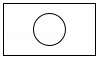
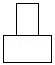
 的值为0,则
的值为0,则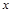 的值为( ).
的值为( ). 中自变量
中自变量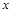 的取值范围为( ).
的取值范围为( ).
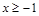
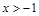

 的解集在数轴上表示为( ).
的解集在数轴上表示为( ).



 的方程
的方程 有一个根为﹣1,则另一个根为( ).
有一个根为﹣1,则另一个根为( ). ∥
∥ ,∠1=120°,则∠2的度数是 .
,∠1=120°,则∠2的度数是 .
 .
. 的解为 .
的解为 .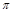 ).
). ,
, ,则
,则 的值为 .
的值为 . ,其中
,其中 ,
, .
. .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号