初中数学规律型：图形的变化类试题

如图，将一枚跳棋放在七边形 $\mathit{ABCDEFG}$ 的顶点 $A$ 处，按顺时针方向移动这枚跳棋2020次．移动规则是：第 $k$ 次移动 $k$ 个顶点（如第一次移动1个顶点，跳棋停留在 $B$ 处，第二次移动2个顶点，跳棋停留在 $D$ 处），按这样的规则，在这2020次移动中，跳棋不可能停留的顶点是 $($ 　　 $)$

A．

$C$ 、 $E$

B．

$E$ 、 $F$

C．

$G$ 、 $C$ 、 $E$

D．

$E$ 、 $C$ 、 $F$

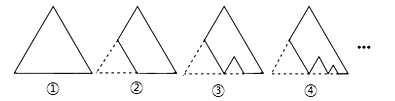
图①是一块边长为1，周长记为的正三角形（三边相等的三角形）纸板，沿图①的底边剪去一块边长为的正三角形纸板后得到图②，然后沿同一底边依次剪去一块更小的正三角形纸板（即其边长为前一块被剪掉正三角形纸板边长的）后，得图③，④，…，记第n（n3）块纸板的周长为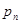，则的值为（  ）

A．

B．

C．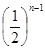

D．

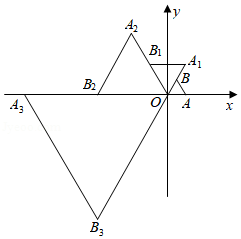
在平面直角坐标系中，等边 $\mathit{\Delta AOB}$ 如图放置，点 $A$ 的坐标为 $(1,0)$ ，每一次将 $\mathit{\Delta AOB}$ 绕着点 $O$ 逆时针方向旋转 $60°$ ，同时每边扩大为原来的2倍，第一次旋转后得到△ $A_{1}O{B}_1$ ，第二次旋转后得到△ $A_{2}O{B}_2$ ， $\dots$ ，依次类推，则点 $A_{2021}$ 的坐标为 $($ 　　 $)$

A．	$(-2^{2020}$ ， $-\sqrt{3}\times 2^{2020})$	B．	$(2^{2021}$ ， $-\sqrt{3}\times 2^{2021})$
C．	$(2^{2020}$ ， $-\sqrt{3}\times 2^{2020})$	D．	$(-2^{2021}$ ， $-\sqrt{3}\times 2^{2021})$

观察下列图形的排列规律（其中、■、★分别表示三角形、正方形、五角星）．若第一个图形是三角形，则第18个图形是           ．（填图形的名称）
■★■★■★■★…

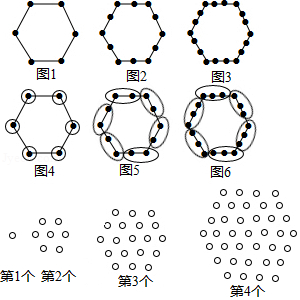
“分块计数法”：对有规律的图形进行计数时，有些题可以采用“分块计数”的方法．

例如：图1有6个点，图2有12个点，图3有18个点， $\dots \dots$，按此规律，求图10、图 $n$有多少个点？

我们将每个图形分成完全相同的6块，每块黑点的个数相同（如图），这样图1中黑点个数是 $6\times 1=6$个；图2中黑点个数是 $6\times 2=12$个：图3中黑点个数是 $6\times 3=18$个； $\dots \dots$；所以容易求出图10、图 $n$中黑点的个数分别是　　、　　．

请你参考以上“分块计数法”，先将下面的点阵进行分块，再完成以下问题：

（1）第5个点阵中有　　个圆圈；第 $n$个点阵中有　　个圆圈．

（2）小圆圈的个数会等于271吗？如果会，请求出是第几个点阵．

观察下列图形，则第个图形中三角形的个数是________

如图，在 $\mathit{\Delta ABC}$中， $\mathit{AB}=5$， $\mathit{AC}=4$，若进行以下操作，在边 $\mathit{BC}$上从左到右依次取点 $D_1$、 $D_2$、 $D_3$、 $D_4$、 $\dots$；过点 $D_1$作 $\mathit{AB}$、 $\mathit{AC}$的平行线分别交 $\mathit{AC}$、 $\mathit{AB}$于点 $E_1$、 $F_1$；过点 $D_2$作 $\mathit{AB}$、 $\mathit{AC}$的平行线分别交 $\mathit{AC}$、 $\mathit{AB}$于点 $E_2$、 $F_2$；过点 $D_3$作 $\mathit{AB}$、 $\mathit{AC}$的平行线分别交 $\mathit{AC}$、 $\mathit{AB}$于点 $E_3$、 $F_3\dots$，则 $4(D_1{E}_1+D_2{E}_2+\dots +D_{2019}{E}_{2019})+5(D_1{F}_1+D_2{F}_2+\dots +D_{2019}{F}_{2019})=$　        　．

如图，已知 $\angle \mathit{AOB}=30°$，在射线 $\mathit{OA}$上取点 $O_1$，以 $O_1$为圆心的圆与 $\mathit{OB}$相切；在射线 $O_{1}A$上取点 $O_2$，以 $O_2$为圆心， $O_2{O}_1$为半径的圆与 $\mathit{OB}$相切；在射线 $O_{2}A$上取点 $O_3$，以 $O_3$为圆心， $O_3{O}_2$为半径的圆与 $\mathit{OB}$相切； $\dots$；在射线 $O_{9}A$上取点 $O_{10}$，以 $O_{10}$为圆心， $O_{10}{O}_9$为半径的圆与 $\mathit{OB}$相切．若 $\odot O_1$的半径为1，则 $\odot O_{10}$的半径长是　　．

如图，自左至右，第1个图由1个正六边形、6个正方形和6个等边三角形组成；第2个图由2个正六边形、11个正方形和10个等边三角形组成；第3个图由3个正六边形、16个正方形和14个等边三角形组成； $\dots$按照此规律，第 $n$个图中正方形和等边三角形的个数之和为　　个．

下列图中所有小正方形都是全等的．图（1）是一张由4个小正方形组成的" $L$ "形纸片，图（2）是一张由6个小正方形组成的 $3\times 2$ 方格纸片．

把" $L$ "形纸片放置在图（2）中，使它恰好盖住其中的4个小正方形，共有如图（3）中的4种不同放置方法．图（4）是一张由36个小正方形组成的 $6\times 6$ 方格纸片，将" $L$ "形纸片放置在图（4）中，使它恰好盖住其中的4个小正方形，共有 $n$ 种不同放置方法，则 $n$ 的值是 $($ 　　 $)$

A．

160

B．

128

C．

80

D．

48

如图各图形是由大小相同的黑点组成，图1中有2个点，图2中有7个点，图3中有14个点，，按此规律，第10个图中黑点的个数是　　．

某广场用同一种如图所示的地砖拼图案，第一次拼成形如图1所示的图案，第二次拼成形如图2所示的图案，第三次拼成形如图3所示的图案，第四次拼成形如图4所示的图案 $\dots$按照这样的规律进行下去，第 $n$次拼成的图案共用地砖　　块．

如图是由同样大小的圆按一定规律排列所组成的，其中第1个图形中一共有4个圆，第2个图形中一共有8个圆，第3个图形中一共有14个圆，第4个图形中一共有22个圆按此规律排列下去，第9个图形中圆的个数是　 　个．

如图，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第20个图需要黑色棋子的个数为　 　．

用黑白两色的正方形纸片，按黑色纸片数逐渐加1的规律拼成一列图案：则第个图案中有白色纸片         张．