初中数学规律型：图形的变化类试题

图1是由若干个小圆圈堆成的一个形如等边三角形的图案，最上面一层有一个圆圈，
以下各层均比上一层多一个圆圈，一共堆了n 层．将图1倒置后与原图1拼成图2的形状，这样我们可以
算出图1中所有圆圈的个数为1＋2＋3＋…＋n＝．

如果图中的圆圈共有13层，请解决下列问题：
（1）我们自上往下，在每个圆圈中按图3的方式填上一串连续的正整数1，2，3，4，……，则最底层最左
边这个圆圈中的数是         ；
（2）我们自上往下，在每个圆圈中按图4的方式填上一串连续的整数－23，－22，－21，－20，……，求
最底层最右边圆圈内的数是_______；
（3）求图4中所有圆圈中各数的绝对值之和．

如图， 第一个图形中有 1 个点， 第二个图形中有 4 个点， 第三个图形中有 13 个点， $\dots$，按此规律， 第 $n$个图形中有　　个点 ．

如图，是用火柴搭的 1条、 2条、 3条“金鱼”……，则搭n条“金鱼”需要火柴            根．

如图，已知 $\angle \mathit{AOB}=30°$，在射线 $\mathit{OA}$上取点 $O_1$，以 $O_1$为圆心的圆与 $\mathit{OB}$相切；在射线 $O_{1}A$上取点 $O_2$，以 $O_2$为圆心， $O_2{O}_1$为半径的圆与 $\mathit{OB}$相切；在射线 $O_{2}A$上取点 $O_3$，以 $O_3$为圆心， $O_3{O}_2$为半径的圆与 $\mathit{OB}$相切； $\dots$；在射线 $O_{9}A$上取点 $O_{10}$，以 $O_{10}$为圆心， $O_{10}{O}_9$为半径的圆与 $\mathit{OB}$相切．若 $\odot O_1$的半径为1，则 $\odot O_{10}$的半径长是　　．

如图，自左至右，第1个图由1个正六边形、6个正方形和6个等边三角形组成；第2个图由2个正六边形、11个正方形和10个等边三角形组成；第3个图由3个正六边形、16个正方形和14个等边三角形组成； $\dots$按照此规律，第 $n$个图中正方形和等边三角形的个数之和为　　个．

下列图中所有小正方形都是全等的．图（1）是一张由4个小正方形组成的" $L$ "形纸片，图（2）是一张由6个小正方形组成的 $3\times 2$ 方格纸片．

把" $L$ "形纸片放置在图（2）中，使它恰好盖住其中的4个小正方形，共有如图（3）中的4种不同放置方法．图（4）是一张由36个小正方形组成的 $6\times 6$ 方格纸片，将" $L$ "形纸片放置在图（4）中，使它恰好盖住其中的4个小正方形，共有 $n$ 种不同放置方法，则 $n$ 的值是 $($ 　　 $)$

A．

160

B．

128

C．

80

D．

48

如图，学校准备新建一个长度为L的读书长廊，并准备用若干块带有花纹和没有花纹的两种规格大小相同的正方形地面砖搭配在一起，按图中所示的规律拼成图案铺满长廊，已知每个小正方形地面砖的边长均为0．5m．

（1）按图示规律，第一图案的长度L₁=m；第二个图案的长度L₂=           m；
（2）用代数式表示带有花纹的地面砖块数n与走廊的长度L_n（m）之间的关系      ；

将一些半径相同的小圆按如图所示的规律摆放，请仔细观察，第 $n$个图形有　 $(n^2+n+4)$　个小圆．（用含 $n$的代数式表示）

观察如图的图形，它们是按一定规律排列的，依照此规律，第（    ）个图形共由120个五角星组成．

A．13

B．14

C．15

D．16

如图各图形是由大小相同的黑点组成，图1中有2个点，图2中有7个点，图3中有14个点，，按此规律，第10个图中黑点的个数是　　．

某广场用同一种如图所示的地砖拼图案，第一次拼成形如图1所示的图案，第二次拼成形如图2所示的图案，第三次拼成形如图3所示的图案，第四次拼成形如图4所示的图案 $\dots$按照这样的规律进行下去，第 $n$次拼成的图案共用地砖　　块．

如图是由同样大小的圆按一定规律排列所组成的，其中第1个图形中一共有4个圆，第2个图形中一共有8个圆，第3个图形中一共有14个圆，第4个图形中一共有22个圆按此规律排列下去，第9个图形中圆的个数是　 　个．

如图，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第20个图需要黑色棋子的个数为　 　．

某餐厅中，一张桌子可坐6人，有以下两种摆放方式：
（1）当有张桌子时，两种摆放方式各能坐多少人？
（2）一天中午餐厅要接待98位顾客共同就餐，但餐厅只有25张这样的餐桌，若你是这个餐厅的经理，你打算选择哪种方式来摆放餐桌，为什么？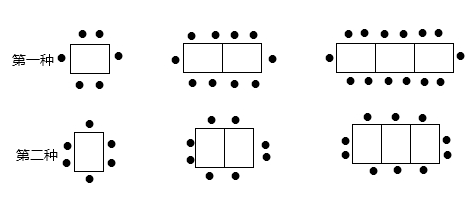

如图，每个图案都由若干个棋子摆成，依照此规律，第n个图案中棋子的总个数可以用含n的代数式表示为           ．