如图,将矩形 绕其右下角的顶点按顺时针方向旋转 至图①位置,继续绕右下角的顶点按顺时针方向旋转 至图②位置,以此类推,这样连续旋转2017次.若 , ,则顶点 在整个旋转过程中所经过的路径总长为

A. B. C. D.
如图,四边形 是边长为1的正方形,以对角线 为边作第二个正方形 ,连接 ,得到△ ;再以对角线 为边作第三个正方形 ,连接 ,得到△ ;再以对角线 为边作第四个正方形,连接 ,得到△ 记△ 、△ 、△ 的面积分别为 、 、 ,如此下去,则 .

如图,四边形 是边长为1的正方形,以对角线 为边作第二个正方形 .连接 ,得到△ ;再以对角线 为边作第三个正方形 ,连接 ,得到△ ;再以对角线 为边作第四个正方形,连接 ,得到△ 记△ 、△ 、△ 的面积分别为 、 、 ,如此下去,则 .

归纳“ ”字形,用棋子摆成的“ ”字形如图所示,按照图①,图②,图③的规律摆下去,摆成第 个“ ”字形需要的棋子个数为 .

将一些圆按照如图方式摆放,从上向下有无数行,其中第一行有2个圆,第二行有4个圆,第三行有6个圆 按此规律排列下去,则前50行共有圆 个.

如图,已知等边 的边长是2,以 边上的高 为边作等边三角形,得到第一个等边△ ;再以等边△ 的 边上的高 为边作等边三角形,得到第二个等边△ ;再以等边△ 的 边上的高 为边作等边三角形,得到第三个等边△ ; ,记△ 的面积为 ,△ 的面积为 ,△ 的面积为 ,如此下去,则 或 .
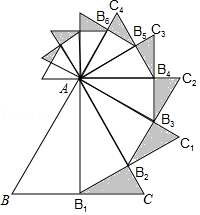
如图,已知等边 的边长是2,以 边上的高 为边作等边三角形,得到第一个等边△ ;再以等边△ 的 边上的高 为边作等边三角形,得到第二个等边△ ;再以等边△ 的 边上的高 为边作等边三角形,得到第三个等边△ ; .记△ 面积为 ,△ 面积为 ,△ 面积为 ,则 .

下面摆放的图案,从第2个起,每一个都是前一个按顺时针方向旋转 得到,第2019个图案与第1个至第4个中的第 个箭头方向相同(填序号).

如图,正方形 的边长为1,以对角线 为边作第二个正方形 ,再以对角线 为边作第三个正方形 ,依此下去,第 个正方形的面积为

A. B. C. D.
如图,下列图案是由火柴棒按某种规律搭成的,第(1)个图案中有2个正方形,第(2)个图案中有5个正方形,第(3)个图案中有8个正方形 ,则第(5)个图案中有 个正方形,第 个图案中有 个正方形.

如图,正方形 的边长为2,其面积标记为 ,以 为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为 , ,按照此规律继续下去,则 的值为

A. B. C. D.
问题提出:用若干相同的一个单位长度的细直木棒,按照如图1方式搭建一个长方体框架,探究所用木棒条数的规律.

问题探究:
我们先从简单的问题开始探究,从中找出解决问题的方法.
探究一
用若干木棒来搭建横长是 ,纵长是 的矩形框架 、 是正整数),需要木棒的条数.
如图①,当 , 时,横放木棒为 条,纵放木棒为 条,共需4条;
如图②,当 , 时,横放木棒为 条,纵放木棒为 条,共需7条;
如图③,当 , 时,横放木棒为 条,纵放木棒为 条,共需12条;
如图④,当 , 时,横放木棒为 条,纵放木棒为 条,共需10条;
如图⑤,当 , 时,横放木棒为 条,纵放木棒为 条,共需17条.

问题(一 :当 , 时,共需木棒 条.
问题(二 :当矩形框架横长是 ,纵长是 时,横放的木棒为 条,
纵放的木棒为 条.
探究二
用若干木棒来搭建横长是 ,纵长是 ,高是 的长方体框架 、 、 是正整数),需要木棒的条数.
如图⑥,当 , , 时,横放与纵放木棒之和为 条,竖放木棒为 条,共需46条;
如图⑦,当 , , 时,横放与纵放木棒之和为 条,竖放木棒为 条,共需75条;
如图⑧,当 , , 时,横放与纵放木棒之和为 条,竖放木棒为 条,共需104条.

问题(三 :当长方体框架的横长是 ,纵长是 ,高是 时,横放与纵放木棒条数之和为 条,竖放木棒条数为 条.
实际应用:现在按探究二的搭建方式搭建一个纵长是2、高是4的长方体框架,总共使用了170条木棒,则这个长方体框架的横长是 .
拓展应用:若按照如图2方式搭建一个底面边长是10,高是5的正三棱柱框架,需要木棒 条.
如图,小正方形是按一定规律摆放的,下面四个选项中的图片,适合填补图中空白处的是

A. B.
B. C.
C. D.
D.
设 的面积为1.
如图1,分别将 , 边2等分, , 是其分点,连接 , 交于点 ,得到四边形 ,其面积 .
如图2,分别将 , 边3等分, , , , 是其分点,连接 , 交于点 ,得到四边形 ,其面积 ;
如图3,分别将 , 边4等分, , , , , , 是其分点,连接 , 交于点 ,得到四边形 ,其面积 ;
按照这个规律进行下去,若分别将 , 边 等分, ,得到四边形 ,其面积 .
