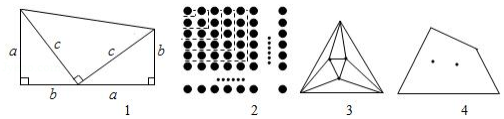
下列图案是用长度相同的火柴棒按一定规律拼搭而成,图案①需8根火柴棒,图案②需15根火柴棒, ,按此规律,图案⑦需 根火柴棒.

观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2018个图形共有 个〇.

已知直线 和直线 ,其中 为不小于2的自然数.
(1)当 时,直线 、 与 轴围成的三角形的面积 ;
(2)当 、3、4, ,2018时,设直线 、 与 轴围成的三角形的面积分别为 , , , , ,则 .
如图所示,将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形,第1幅图形中“●”的个数为 ,第2幅图形中“●”的个数为 ,第3幅图形中“●”的个数为 , ,以此类推,则 的值为

A. B. C. D.
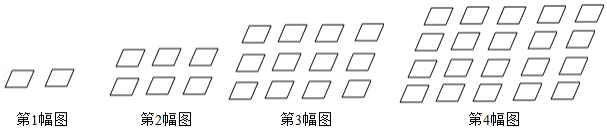
如图所示,下列图形都是由相同的玫瑰花按照一定的规律摆成的,按此规律摆下去,第 个图形中有120朵玫瑰花,则 的值为
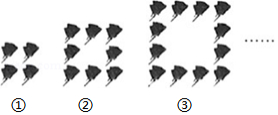
A.28B.29C.30D.31
如图,点 的坐标为 ,过点 作 轴的垂线交直线 于点 ,以原点 为圆心, 的长为半径画弧交 轴正半轴于点 ;再过点 作 轴的垂线交直线 于点 ,以原点 为圆心,以 的长为半径画弧交 轴正半轴于点 ; .按此作法进行下去,则 的长是 .

我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10…)和“正方形数”(如1,4,9,16…),在小于200的数中,设最大的“三角形数”为 ,最大的“正方形数”为 ,则 的值为
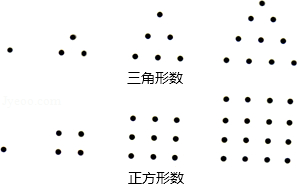
A.33B.301C.386D.571
庄子说:“一尺之椎,日取其半,万世不竭”.这句话(文字语言)表达了古人将事物无限分割的思想,用图形语言表示为图1,按此图分割的方法,可得到一个等式(符号语言) .

图2也是一种无限分割:在 中, , ,过点 作 于点 ,再过点 作 于点 ,又过点 作 于点 ,如此无限继续下去,则可将利 分割成 、△ 、△ 、△ 、 、△ 、 .假设 ,这些三角形的面积和可以得到一个等式是 .
如图,在平面直角坐标系 中,直线 分别与 轴、 轴交于点 、 ,在 中从左向右依次作正方形 、 、 ,点 、 、 在 轴上,点 在 轴上,点 、 、 在直线 上;再将每个正方形分割成四个全等的直角三角形和一个小正方形,其中每个小正方形的边都与坐标轴平行,从左至右的小正方形(阴影部分)的面积分别记为 、 、 ,则 可表示为

A.. B..
C.. D..
在公园内,牡丹按正方形种植,在它的周围种植芍药,如图反映了牡丹的列数 和芍药的数量规律,那么当 时,芍药的数量为
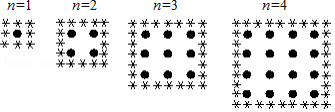
A.84株B.88株C.92株D.121株
如图所示,将形状大小完全相同的“ ”按照一定规律摆成下列图形,第1幅图中“ ”的个数为 ,第2幅图中“ ”的个数为 ,第3幅图中“ ”的个数为 , ,以此类推,若 . 为正整数),则 的值为 .
如图,在 中, , ,若进行以下操作,在边 上从左到右依次取点 、 、 、 、 ;过点 作 、 的平行线分别交 、 于点 、 ;过点 作 、 的平行线分别交 、 于点 、 ;过点 作 、 的平行线分别交 、 于点 、 ,则 .

(阅读)
数学中,常对同一个量(图形的面积、点的个数、三角形的内角和等)用两种不同的方法计算,从而建立相等关系,我们把这一思想称为“算两次”.“算两次”也称做富比尼原理,是一种重要的数学思想.
(理解)
(1)如图1,两个直角边长分别为 、 、斜边长为 的直角三角形和一个两条直角边都是 的直角三角形拼成一个梯形.用两种不同的方法计算梯形的面积,并写出你发现的结论;
(2)如图2, 行 列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式: ;
(运用)
(3) 边形有 个顶点,在它的内部再画 个点,以 个点为顶点,把 边形剪成若干个三角形,设最多可以剪得 个这样的三角形.当 , 时,如图3,最多可以剪得7个这样的三角形,所以 .
①当 , 时,如图4, ;当 , 时, ;
②对于一般的情形,在 边形内画 个点,通过归纳猜想,可得 (用含 、 的代数式表示).请对同一个量用算两次的方法说明你的猜想成立.