庄子说:“一尺之椎,日取其半,万世不竭”.这句话(文字语言)表达了古人将事物无限分割的思想,用图形语言表示为图1,按此图分割的方法,可得到一个等式(符号语言) .
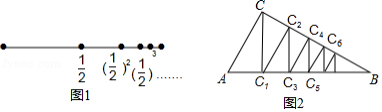
图2也是一种无限分割:在 中, , ,过点 作 于点 ,再过点 作 于点 ,又过点 作 于点 ,如此无限继续下去,则可将利 分割成 、△ 、△ 、△ 、 、△ 、 .假设 ,这些三角形的面积和可以得到一个等式是 .
相关知识点
推荐套卷
庄子说:“一尺之椎,日取其半,万世不竭”.这句话(文字语言)表达了古人将事物无限分割的思想,用图形语言表示为图1,按此图分割的方法,可得到一个等式(符号语言) .
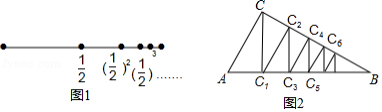
图2也是一种无限分割:在 中, , ,过点 作 于点 ,再过点 作 于点 ,又过点 作 于点 ,如此无限继续下去,则可将利 分割成 、△ 、△ 、△ 、 、△ 、 .假设 ,这些三角形的面积和可以得到一个等式是 .