设 的面积为1.
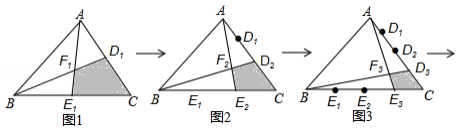
如图1,分别将 , 边2等分, , 是其分点,连接 , 交于点 ,得到四边形 ,其面积 .
如图2,分别将 , 边3等分, , , , 是其分点,连接 , 交于点 ,得到四边形 ,其面积 ;
如图3,分别将 , 边4等分, , , , , , 是其分点,连接 , 交于点 ,得到四边形 ,其面积 ;
按照这个规律进行下去,若分别将 , 边 等分, ,得到四边形 ,其面积 .
相关知识点
推荐套卷
设 的面积为1.
如图1,分别将 , 边2等分, , 是其分点,连接 , 交于点 ,得到四边形 ,其面积 .
如图2,分别将 , 边3等分, , , , 是其分点,连接 , 交于点 ,得到四边形 ,其面积 ;
如图3,分别将 , 边4等分, , , , , , 是其分点,连接 , 交于点 ,得到四边形 ,其面积 ;
按照这个规律进行下去,若分别将 , 边 等分, ,得到四边形 ,其面积 .
