在公园内,牡丹按正方形种植,在它的周围种植芍药,如图反映了牡丹的列数 和芍药的数量规律,那么当 时,芍药的数量为
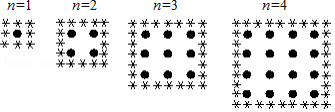
A.84株B.88株C.92株D.121株
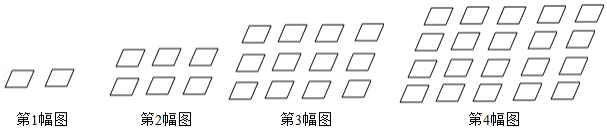
如图所示,将形状大小完全相同的“ ”按照一定规律摆成下列图形,第1幅图中“ ”的个数为 ,第2幅图中“ ”的个数为 ,第3幅图中“ ”的个数为 , ,以此类推,若 . 为正整数),则 的值为 .
如图,在 中, , ,若进行以下操作,在边 上从左到右依次取点 、 、 、 、 ;过点 作 、 的平行线分别交 、 于点 、 ;过点 作 、 的平行线分别交 、 于点 、 ;过点 作 、 的平行线分别交 、 于点 、 ,则 .

(阅读)
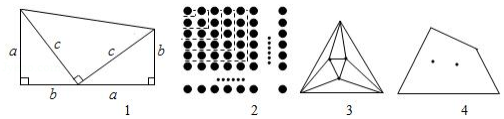
数学中,常对同一个量(图形的面积、点的个数、三角形的内角和等)用两种不同的方法计算,从而建立相等关系,我们把这一思想称为“算两次”.“算两次”也称做富比尼原理,是一种重要的数学思想.
(理解)
(1)如图1,两个直角边长分别为 、 、斜边长为 的直角三角形和一个两条直角边都是 的直角三角形拼成一个梯形.用两种不同的方法计算梯形的面积,并写出你发现的结论;
(2)如图2, 行 列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式: ;
(运用)
(3) 边形有 个顶点,在它的内部再画 个点,以 个点为顶点,把 边形剪成若干个三角形,设最多可以剪得 个这样的三角形.当 , 时,如图3,最多可以剪得7个这样的三角形,所以 .
①当 , 时,如图4, ;当 , 时, ;
②对于一般的情形,在 边形内画 个点,通过归纳猜想,可得 (用含 、 的代数式表示).请对同一个量用算两次的方法说明你的猜想成立.
如图,将矩形 绕其右下角的顶点按顺时针方向旋转 至图①位置,继续绕右下角的顶点按顺时针方向旋转 至图②位置,以此类推,这样连续旋转2017次.若 , ,则顶点 在整个旋转过程中所经过的路径总长为

A. B. C. D.
如图,四边形 是边长为1的正方形,以对角线 为边作第二个正方形 ,连接 ,得到△ ;再以对角线 为边作第三个正方形 ,连接 ,得到△ ;再以对角线 为边作第四个正方形,连接 ,得到△ 记△ 、△ 、△ 的面积分别为 、 、 ,如此下去,则 .

如图,四边形 是边长为1的正方形,以对角线 为边作第二个正方形 .连接 ,得到△ ;再以对角线 为边作第三个正方形 ,连接 ,得到△ ;再以对角线 为边作第四个正方形,连接 ,得到△ 记△ 、△ 、△ 的面积分别为 、 、 ,如此下去,则 .

归纳“ ”字形,用棋子摆成的“ ”字形如图所示,按照图①,图②,图③的规律摆下去,摆成第 个“ ”字形需要的棋子个数为 .

将一些圆按照如图方式摆放,从上向下有无数行,其中第一行有2个圆,第二行有4个圆,第三行有6个圆 按此规律排列下去,则前50行共有圆 个.

如图,已知等边 的边长是2,以 边上的高 为边作等边三角形,得到第一个等边△ ;再以等边△ 的 边上的高 为边作等边三角形,得到第二个等边△ ;再以等边△ 的 边上的高 为边作等边三角形,得到第三个等边△ ; ,记△ 的面积为 ,△ 的面积为 ,△ 的面积为 ,如此下去,则 或 .
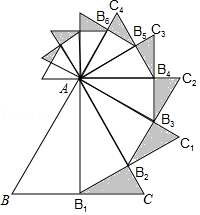
如图,已知等边 的边长是2,以 边上的高 为边作等边三角形,得到第一个等边△ ;再以等边△ 的 边上的高 为边作等边三角形,得到第二个等边△ ;再以等边△ 的 边上的高 为边作等边三角形,得到第三个等边△ ; .记△ 面积为 ,△ 面积为 ,△ 面积为 ,则 .

下面摆放的图案,从第2个起,每一个都是前一个按顺时针方向旋转 得到,第2019个图案与第1个至第4个中的第 个箭头方向相同(填序号).

如图,正方形 的边长为1,以对角线 为边作第二个正方形 ,再以对角线 为边作第三个正方形 ,依此下去,第 个正方形的面积为

A. B. C. D.