初中数学规律型：图形的变化类试题

如图，正方形 $\mathit{ABCD}$的边长为2，其面积标记为 $S_1$，以 $\mathit{CD}$为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为 $S_2$， $\dots$，按照此规律继续下去，则 $S_9$的值为 $($　　 $)$

A． ${\left(\frac{1}{2}\right)}^6$B． ${\left(\frac{1}{2}\right)}^7$C． ${\left(\frac{\sqrt{2}}{2}\right)}^6$D． ${\left(\frac{\sqrt{2}}{2}\right)}^7$

问题提出：用若干相同的一个单位长度的细直木棒，按照如图1方式搭建一个长方体框架，探究所用木棒条数的规律．

问题探究：

我们先从简单的问题开始探究，从中找出解决问题的方法．

探究一

用若干木棒来搭建横长是 $m$，纵长是 $n$的矩形框架 $(m$、 $n$是正整数），需要木棒的条数．

如图①，当 $m=1$， $n=1$时，横放木棒为 $1\times (1+1)$条，纵放木棒为 $(1+1)\times 1$条，共需4条；

如图②，当 $m=2$， $n=1$时，横放木棒为 $2\times (1+1)$条，纵放木棒为 $(2+1)\times 1$条，共需7条；

如图③，当 $m=2$， $n=2$时，横放木棒为 $2\times (2+1)$条，纵放木棒为 $(2+1)\times 2$条，共需12条；

如图④，当 $m=3$， $n=1$时，横放木棒为 $3\times (1+1)$条，纵放木棒为 $(3+1)\times 1$条，共需10条；

如图⑤，当 $m=3$， $n=2$时，横放木棒为 $3\times (2+1)$条，纵放木棒为 $(3+1)\times 2$条，共需17条．

问题（一 $)$：当 $m=4$， $n=2$时，共需木棒　　条．

问题（二 $)$：当矩形框架横长是 $m$，纵长是 $n$时，横放的木棒为　　条，

纵放的木棒为　　条．

探究二

用若干木棒来搭建横长是 $m$，纵长是 $n$，高是 $s$的长方体框架 $(m$、 $n$、 $s$是正整数），需要木棒的条数．

如图⑥，当 $m=3$， $n=2$， $s=1$时，横放与纵放木棒之和为 $[3\times (2+1)+(3+1)\times 2]\times (1+1)=34$条，竖放木棒为 $(3+1)\times (2+1)\times 1=12$条，共需46条；

如图⑦，当 $m=3$， $n=2$， $s=2$时，横放与纵放木棒之和为 $[3\times (2+1)+(3+1)\times 2]\times (2+1)=51$条，竖放木棒为 $(3+1)\times (2+1)\times 2=24$条，共需75条；

如图⑧，当 $m=3$， $n=2$， $s=3$时，横放与纵放木棒之和为 $[3\times (2+1)+(3+1)\times 2]\times (3+1)=68$条，竖放木棒为 $(3+1)\times (2+1)\times 3=36$条，共需104条．

问题（三 $)$：当长方体框架的横长是 $m$，纵长是 $n$，高是 $s$时，横放与纵放木棒条数之和为　　条，竖放木棒条数为　　条．

实际应用：现在按探究二的搭建方式搭建一个纵长是2、高是4的长方体框架，总共使用了170条木棒，则这个长方体框架的横长是　　．

拓展应用：若按照如图2方式搭建一个底面边长是10，高是5的正三棱柱框架，需要木棒　　条．

如图，小正方形是按一定规律摆放的，下面四个选项中的图片，适合填补图中空白处的是 $($　　 $)$

A．B．C．D．

设 $\mathit{\Delta ABC}$的面积为1．

如图1，分别将 $\mathit{AC}$， $\mathit{BC}$边2等分， $D_1$， $E_1$是其分点，连接 $A{E}_1$， $B{D}_1$交于点 $F_1$，得到四边形 $C{D}_1{F}_1{E}_1$，其面积 $S_1=\frac{1}{3}$．

如图2，分别将 $\mathit{AC}$， $\mathit{BC}$边3等分， $D_1$， $D_2$， $E_1$， $E_2$是其分点，连接 $A{E}_2$， $B{D}_2$交于点 $F_2$，得到四边形 $C{D}_2{F}_2{E}_2$，其面积 $S_2=\frac{1}{6}$；

如图3，分别将 $\mathit{AC}$， $\mathit{BC}$边4等分， $D_1$， $D_2$， $D_3$， $E_1$， $E_2$， $E_3$是其分点，连接 $A{E}_3$， $B{D}_3$交于点 $F_3$，得到四边形 $C{D}_3{F}_3{E}_3$，其面积 $S_3=\frac{1}{10}$；

$\dots$

按照这个规律进行下去，若分别将 $\mathit{AC}$， $\mathit{BC}$边 $(n+1)$等分， $\dots$，得到四边形 $C{D}_n{F}_n{E}_n$，其面积 $S_n=$　　．

用棋子摆出下列一组图形：

按照这种规律摆下去，第 $n$个图形用的棋子个数为 $($　　 $)$

A． $3n$B． $6n$C． $3n+6$D． $3n+3$

如图，自左至右，第1个图由1个正六边形、6个正方形和6个等边三角形组成；第2个图由2个正六边形、11个正方形和10个等边三角形组成；第3个图由3个正六边形、16个正方形和14个等边三角形组成； $\dots$按照此规律，第 $n$个图中正方形和等边三角形的个数之和为　　个．

某广场用同一种如图所示的地砖拼图案，第一次拼成形如图1所示的图案，第二次拼成形如图2所示的图案，第三次拼成形如图3所示的图案，第四次拼成形如图4所示的图案 $\dots$按照这样的规律进行下去，第 $n$次拼成的图案共用地砖　　块．

将一些相同的“〇”按如图所示摆放，观察每个图形中的“〇”的个数，若第 $n$个图形中“〇”的个数是78，则 $n$的值是 $($　　 $)$

A．11B．12C．13D．14

如图，在平面直角坐标系中，直线 $l$的函数表达式为 $y=x$，点 $O_1$的坐标为 $(1,0)$，以 $O_1$为圆心， $O_{1}O$为半径画圆，交直线 $l$于点 $P_1$，交 $x$轴正半轴于点 $O_2$，以 $O_2$为圆心， $O_{2}O$为半径画圆，交直线 $l$于点 $P_2$，交 $x$轴正半轴于点 $O_3$，以 $O_3$为圆心， $O_{3}O$为半径画圆，交直线 $l$于点 $P_3$，交 $x$轴正半轴于点 $O_4$； $\dots$按此做法进行下去，其中 $\stackrel{̂}{P_{2017}{O}_{2018}}$的长为　　．

观察下列图形，它是把一个三角形分别连接这个三角形三边的中点，构成4个小三角形，挖去中间的一个小三角形（如图 $1)$；对剩下的三个小三角形再分别重复以上做法， $\dots$将这种做法继续下去（如图2，图 $3\dots )$，则图6中挖去三角形的个数为 $($　　 $)$

A．121B．362C．364D．729

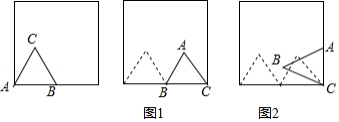
如图，边长为1的正三角形 $\mathit{ABC}$放置在边长为2的正方形内部，顶点 $A$在正方形的一个顶点上，边 $\mathit{AB}$在正方形的一边上，将 $\mathit{\Delta ABC}$绕点 $B$顺时针旋转，当点 $C$落在正方形的边上时，完成第1次无滑动滚动（如图 $1)$；再将 $\mathit{\Delta ABC}$绕点 $C$顺时针旋转，当点 $A$落在正方形的边上时，完成第2次无滑动滚动（如图 $2)$， $\dots$，每次旋转的角度都不大于 $120°$，依次这样操作下去，当完成第2016次无滑动滚动时，点 $A$经过的路径总长为　　．

如图，在平面直角坐标系中， $\angle \mathit{MO}{A}_1=30°$，四边形 $A_1{B}_1{C}_1{B}_2$， $A_2{B}_2{C}_2{B}_3$， $A_3{B}_3{C}_3{B}_4\dots \dots A_n{B}_n{C}_n{B}_{n+1}$都是菱形，点 $A_1$， $A_2$， $A_3\dots \dots A_n$在 $x$轴上，点 $B_1$， $B_2$， $B_3\dots \dots B_{n+1}$在 $\mathit{OM}$上， $B_1{C}_1//B_2{C}_2//B_3{C}_3\dots \dots B_n{C}_n//y$轴， $A_1{B}_1=\sqrt{2}$，则第 $n$个菱形 $A_n{B}_n{C}_n{B}_{n+1}$的面积是　　．

观察下列图形：

它们是按一定规律排列的，依照此规律，第 $n$个图中共有　　个★．

如图，面积为1的等腰直角△ $O{A}_1{A}_2$， $\angle O{A}_2{A}_1=90°$，且 $O{A}_2$为斜边在△ $O{A}_1{A}_2$，外作等腰直角△ $O{A}_2{A}_3$，以 $O{A}_3$为斜边在△ $O{A}_2{A}_3$，外作等腰直角△ $O{A}_3{A}_4$，以 $O{A}_4$为斜边在△ $O{A}_3{A}_4$，外作等腰直角△ $O{A}_4{A}_5$， $\dots$连接 $A_1{A}_3$， $A_3{A}_5$， $A_5{A}_7$， $\dots$分别与 $O{A}_2$， $O{A}_4$， $O{A}_6$， $\dots$交于点 $B_1$， $B_2$， $B_3$， $\dots$按此规律继续下去，记△ $O{B}_1{A}_3$的面积为 $S_1$，△ $O{B}_2{A}_5$的面积为 $S_2$，△ $O{B}_3{A}_7$的面积为 $S_3$， $\dots$△ $O{B}_n{A}_{2n+1}$的面积为 $S_n$，则 $S_n=$　　（用含正整数 $n$的式子表示）．

如图， $\mathit{\Delta ABC}$的面积为 $S$．点 $P_1$， $P_2$， $P_3$， $\dots$， $P_{n-1}$是边 $\mathit{BC}$的 $n$等分点 $(n⩾3$，且 $n$为整数），点 $M$， $N$分别在边 $\mathit{AB}$， $\mathit{AC}$上，且 $\frac{\mathit{AM}}{\mathit{AB}}=\frac{\mathit{AN}}{\mathit{AC}}=\frac{1}{n}$，连接 $M{P}_1$， $M{P}_2$， $M{P}_3$， $\dots$， $M{P}_{n-1}$，连接 $\mathit{NB}$， $N{P}_1$， $N{P}_2$， $\dots$， $N{P}_{n-1}$，线段 $M{P}_1$与 $\mathit{NB}$相交于点 $D_1$，线段 $M{P}_2$与 $N{P}_1$相交于点 $D_2$，线段 $M{P}_3$与 $N{P}_2$相交于点 $D_3$， $\dots$，线段 $M{P}_{n-1}$与 $N{P}_{n-2}$相交于点 $D_{n-1}$，则△ $N{D}_1{P}_1$，△ $N{D}_2{P}_2$，△ $N{D}_3{P}_3$， $\dots$，△ $N{D}_{n-1}{P}_{n-1}$的面积和是　　．（用含有 $S$与 $n$的式子表示）