初中数学规律型：图形的变化类试题

如图，在 $\mathit{\Delta OAB}$ 中，顶点 $O(0,0)$ ， $A(-3,4)$ ， $B(3,4)$ ，将 $\mathit{\Delta OAB}$ 与正方形 $\mathit{ABCD}$ 组成的图形绕点 $O$ 顺时针旋转，每次旋转 $90°$ ，则第70次旋转结束时，点 $D$ 的坐标为 $($ 　　 $)$

A．

$(10,3)$

B．

$(-3,10)$

C．

$(10,-3)$

D．

$(3,-10)$

（1）观察下列图形与等式的关系，并填空

（2）观察下图，根据（1）中结论，计算图中黑球的个数，用含有的代数式填空：

　　　　．

如图，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第五个图形需要黑色棋子的个数是      ，第n个图形需要黑色棋子的个数是      （n≥1，且n为整数）．

如图所示，AB=16cm，

（1）若C₁是AB的中点，求AC₁的长度
（2）若C₂是A C₁的中点，求AC₂的长度
（3）若C₃是A C₂的中点，求AC₃的长度
（4）若照上述规律发展下去，则AC_n的长度是多少呢？

有一个正六面体骰子（如图a）放在桌面上，将骰子沿如图所示的顺时针方向滚动，每滚动90°算一次，则滚动第2015次后，骰子朝下一面的点数是            ．

下列图形都是由同样大小的五角星按一定的规律组成，其中第①个图形一共有2个五角星，第②个图形一共有8个五角星，第③个图形一共有18个五角星，…，则第⑥个图形中五角星的个数为（ ）

A．50

B．64

C．68

D．72

如图是一组有规律的图案，第1个图案由4个基础图形组成，第2个图案由7个基础图形组成，……，第（是正整数)个图案中由                个基础图形组成．
 

用●表示实圆，用○表示空心圆，现有若干个实圆与空心圆按一定规律排列如下：●○●●○●●●○●○●●○●●●○●○●●○●●●○……问：前2011个圆中，有________个空心圆．

A．670

B．668

C．669

D．671

如图，每一幅图中均含有若干个正方形，第1幅图中有1个正方形；第2幅图中有5个正方形；…按这样的规律下去，第7幅图中有       个正方形．

下列图形都是由同样大小的小圆圈按一定规律所组成的，其中第个图形中一共有6个小圆圈，其中第个图形中一共有9个小圆圈，其中第个图形中一共有12个小圆圈，…，按此规律排列，则第n个图形中小圆圈的个数为__________．

在数学的学习过程中，我们经常用以下的探索过程解决相关问题．
数学问题：三角形有3个顶点，如果在它的内部再画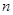个点，并以这个点为顶点画三角形，那么可以剪得多少个这样的三角形？

探索规律：为了解决这个问题，我们可以从、、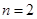等具体的、简单的情形入手，探索最多可以剪得的三角形个数的变化规律．
（1）填表：当三角形内有4个点时，把表格补充完整；
（2）你发现的变化规律是：     ；
（3）猜想：当三角形内点的个数为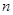时，最多可以剪得        个三角形；
像这样通过对简单情形的观察、分析，从特殊到一般地探索这类现象的规律、提出猜想的思想方法称为归纳．
问题解决：请你尝试用归纳的方法探索的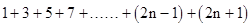和是多少？

如图，线段AB上的点数与线段的总数有如下关系：如果线段AB上有1个点时，线段总共有3条，如果线段AB上有2个点时，线段总数有6条，如果线段AB上有3个点时，线段总数共有10条，…

（1）当线段AB上有6个点时，线段总数共有      条．
（2）当线段AB上有n个点时，线段总数共有      条。
（3）如果从一个多边形的一个顶点出发，分别连接这个顶点与其余各顶点，可将这个多边形分割成2003个三角形，那么此多边形的边数为多少？

小强用黑白两种颜色的正六边形地面砖按如图拼成了三个图案，他发现了规律，若继续这样拼出第4个，第5个，…，那么第n个图案中白色地面砖有________块．

如图，一只青蛙在圆周上标有数字的五个点上跳，若它停在奇数点上，则下一次沿顺时针方向跳两个点；若停在偶数点上，则下一次沿逆时针方向跳一个点．若青蛙从数1这点开始跳，第1次跳到数3那个点，如此，则经2015次跳后它停的点所对应的数为      

如图，小红作出了边长为1的第1个正△A₁B₁C₁，算出了正△A₁B₁C₁的面积，然后分别取△A₁B₁C₁三边的中点A₂，B₂，C₂，作出了第2个正△A₂B₂C₂，算出了正△A₂B₂C₂的面积，用同样的方法，作出了第3个正△A₃B₃C₃，算出了正△A₃B₃C₃的面积…，由此可得，第2014个正△A₂₀₁₄B₂₀₁₄C₂₀₁₄的面积是（  ）

A．	B．
C．	D．