初中数学规律型：数字的变化类试题

观察下列等式：
1、4²-1²=3×5；
2、5²-2²=3×7；
3、6²-3²=3×9；
4、7²-4²=3×11；
…
则第n（n是正整数）个等式为             ．

将从1开始的连续自然数按图规律排列：规定位于第 $m$行，第 $n$列的自然数10记为 $(3,2)$，自然数15记为 $(4,2)\dots$按此规律，自然数2018记为　　

列 行	第1列	第2列	第3列	第4列
第1行	1	2	3	4
第2行	8	7	6	5
第3行	9	10	11	12
第4行	16	15	14	13
$\dots$	$\dots$	$\dots$	$\dots$	$\dots$
第 $n$行	$\dots$	$\dots$	$\dots$	$\dots$

观察下列等式：，，；将以上三个等式两边分别相加得：．
（1）猜想并写出：．
（2）直接写出下列各式的计算结果：
①；
②．
（3）探究并计算式子：的值．

观察下列等式：

在上述数字宝塔中，从上往下数，2016在第　　层．

定义一种新运算，满足下列等式，请你细心观察下列各式：



      
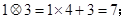
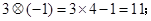
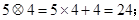
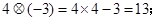
（1）仿照上面式子你可得出：=____________________；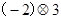
（2）经过探究你可猜想： _____________________；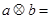
（3）如果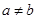，上面你所得到的算式满足交换律吗？为什么？
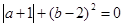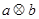（4）如果，试求的值．

如图，将1～2025这2025个自然数按图中规律分别排列在网格中，除对角线AB经过的45个数外，其它的数被分成两部分，对角线AB右上方的990个数之和记为S₁，对角线AB左下方的990个数之和记为S₂．则S₁﹣S₂=      ．

观察下面三行数：
-2，4，-8，16，-32，64…；
0，6，-6，18，-30，66…；
1，-，，-，，-，…；
（1）第一行数的第8个数为        ；
（2）若第一行的第n个数用（-2）ⁿ表示，则第三行的第n个数表示为  ；
（3）取每一行的第m个数，三个数的和记为p，
①当m=10时，求p的值；
②当m=     时，|p+30000|的值最小．

某城市大剧院地面的一部分为扇形，观众席的座位按下列方式设置：

排数	1	2	3	4
座位数	50	53	56	59

 
按这种方式排下去，
（1）第5、6排各有多少个座位？
（2）第n排有多少个座位？
（3）根据（2）的代数式，判断第25排有多少个座位？

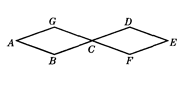
如图所示，两个全等菱形的边长为1厘米，一只蚂蚁由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动，行走2015厘米后停下，则这只蚂蚁停在        点．

观察下面一列数的规律，在横线上填上适当的数：-6，-1，4，9，14，______，______．

观察下列各式的规律：

（a﹣b）（a+b）＝a²﹣b²

（a﹣b）（a²+ab+b²）＝a³﹣b³

（a﹣b）（a³+a²b+ab²+b³）＝a⁴﹣b⁴

…

可得到（a﹣b）（a²⁰¹⁶+a²⁰¹⁵b+…+ab²⁰¹⁵+b²⁰¹⁶）＝　　．

生活中常用的十进制是用 $0~9$ 这十个数字来表示数，满十进一，例： $12=1\times 10+2$ ， $212=2\times 10\times 10+1\times 10+2$ ；计算机也常用十六进制来表示字符代码，它是用 $0~F$ 来表示 $0~15$ ，满十六进一，它与十进制对应的数如表：

十进制	0	1	2	$\dots$	8	9	10	11	12	13	14	15	16	17	$\dots$
十六进制	0	1	2	$\dots$	8	9	$A$	$B$	$C$	$D$	$E$	$F$	10	11	$\dots$

例：十六进制 $2B$ 对应十进制的数为 $2\times 16+11=43$ ， $10C$ 对应十进制的数为 $1\times 16\times 16+0\times 16+12=268$ ，那么十六进制中 $14E$ 对应十进制的数为 $($ 　　 $)$

A．

28

B．

62

C．

238

D．

334

将从1开始的自然数按以下规律排列，例如位于第3行、第4列的数是12，则位于第45行、第8列的数是　　．

我国南宋数学家杨辉所著的《详解九章算术》一书中，用如图的三角形解释二项式 ${(a+b)}^n$的展开式的各项系数，此三角形称为“杨辉三角”

根据”杨辉三角”请计算 ${(a+b)}^8$的展开式中从左起第四项的系数为 $($　　 $)$

A．84B．56C．35D．28

2017年，随州学子尤东梅参加《最强大脑》节目，成功完成了高难度的项目挑战，展现了惊人的记忆力．在2019年的《最强大脑》节目中，也有很多具有挑战性的比赛项目，其中《幻圆》这个项目充分体现了数学的魅力．如图是一个最简单的二阶幻圆的模型，要求：①内、外两个圆周上的四个数字之和相等；②外圆两直径上的四个数字之和相等，则图中两空白圆圈内应填写的数字从左到右依次为　　和　　．