请先阅读下列一组内容,然后解答问题:
因为: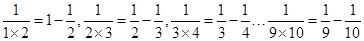
所以: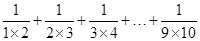
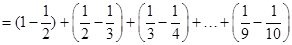
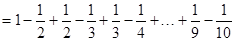
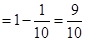
计算:①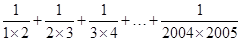 ;
;
②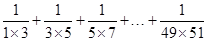
规律探究.下面有8个算式,排成4行2列
2+2, 2×2
3+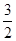 , 3×
, 3×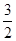
4+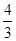 , 4×
, 4×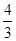
5+ , 5×
, 5× ……, ……
……, ……
(1)同一行中两个算式的结果怎样?
(2)算式2005+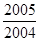 和2005×
和2005×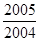 的结果相等吗?
的结果相等吗?
(3)请你试写出算式,试一试,再探索其规律,并用含自然数n的代数式表示这一规律.
给出依次排列的一列数:
—1、2、—4、8、—16、32,---------
(1)按照给出的这个数列的某种规律,继续写出后面的3项: , , ;
(2)这一列数第n个数是什么?
定义一种新运算:观察下列各式:1⊙3=1×4+3=7 ;3⊙(-1)= 3×4-1=11;5⊙4="5×4+4=24" ;4⊙(-3)= 4×4-3=13
(1)请你想一想:用代数式表示a⊙b的结果为:___________;
(2)若a≠b,那么a⊙b______b⊙a(填入“=”或“≠ ”);
(3)若a⊙(-2b)= 4,请计算(a-b)⊙(2a+b)的值.
如图的数阵是由一些奇数组成的.
(1)如图框中的四个数中,若设第一行的第一个数为x,用含x的代数式表示另外三个数;
(2)若这样框中的四个数的和是200,求出这四个数;
(3)是否存在这样的四个数,他们的和为2014?若存在,请求出中四个数中最大的数;若不存在,请说明理由.
阅读下文,寻找规律.计算
 ,
,
 ,
,
 …….
…….
(1)观察上式,并猜想: .
.
(2)根据你的猜想,计算: .(其中n是正整数)
.(其中n是正整数)
观察一列数:1、2、4、8、16、…我们发现,这一列数从第二项起,每一项与它前一项的比都等于2.一般地,如果一列数从第二项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数就叫做等比数列的公比.
(1)等比数列5、﹣15、45、…的第4项是 .
(2)如果一列数a1,a2,a3,a4是等比数列,且公比为q.那么有:a2=a1q,a3=a2q=(a1q)q=a1q2,a4=a3q=(a1q2)q=a1q3
则:a5= .(用a1与q的式子表示)
(3)一个等比数列的第2项是10,第4项是40,求它的公比.
观察下列各式:
﹣1× =﹣1+
=﹣1+
﹣ ×
× =﹣
=﹣ +
+
﹣ ×
×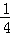 =﹣
=﹣ +
+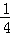
…
(1)你能探索出什么规律?(用文字或表达式)
(2)试运用你发现的规律计算:
(﹣1× )+(﹣
)+(﹣ ×
× )+(﹣
)+(﹣ ×
×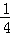 )+…+(﹣
)+…+(﹣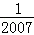 ×
×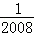 )+(﹣
)+(﹣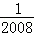 ×
×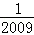 )
)
观察下列各式:
13+23= ;
;
13+23+33=36= ;
;
13+23+33+43=100= ;
;
(1)计算:13+23+33+43+53的值;
(2)计算:13+23+33+43+…+103的值;
(3)猜想:13+23+33+43+…+n3的值.
观察下列等式: ,
, ,
, ;将以上三个等式两边分别相加得:
;将以上三个等式两边分别相加得: .
.
(1)猜想并写出: .
.
(2)直接写出下列各式的计算结果:
① ;
;
② .
.
(3)探究并计算式子: 的值.
的值.
仔细观察下列三组数:
第一组:1,4,9,16,25,…
第二组:1,8,27,64,125,…
第三组:﹣2,﹣8,﹣18,﹣32,﹣50,…
(1)写出每组的第6个数各是多少?
(2)第二组的第100个数是第一组的第100个数的多少倍?
(3)取每组数的第n个数,计算这三个数的和.
定义一种新运算,满足下列等式,请你细心观察下列各式:
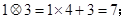
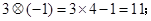
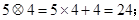
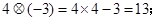
(1)仿照上面式子你可得出: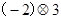 =____________________;
=____________________;
(2)经过探究你可猜想: 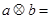 _____________________;
_____________________;
(3)如果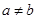 ,上面你所得到的算式满足交换律吗?为什么?
,上面你所得到的算式满足交换律吗?为什么?
(4)如果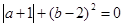 ,试求
,试求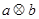 的值.
的值.
观察下面三行数:
-2,4,-8,16,-32,64…;
0,6,-6,18,-30,66…;
1,- ,
, ,-
,- ,
, ,-
,- ,…;
,…;
(1)第一行数的第8个数为 ;
(2)若第一行的第n个数用(-2)n表示,则第三行的第n个数表示为 ;
(3)取每一行的第m个数,三个数的和记为p,
①当m=10时,求p的值;
②当m= 时,|p+30000|的值最小.