初中数学列代数式解答题

重百商场正销售某品牌的一款等离子宽屏幕电视机，年初时售价定为元，3月份售价降低了元．由于伦敦奥运会的举行，8月份销售看好，故商场决定将售价在3月份的基础上上涨10%．奥运会结束后，由于销售不畅，故商场决定将售价在8月份的基础上下调10%．
（1）请用代数式表示该款等离子宽屏幕电视机现在的价格；
（2）若年初时售价定为6500元，3月初售价降低了500元，那么该款等离子宽屏幕电视机现在的价格是多少元？

三角形一边长是cm，第二边比第一边长，第三边比第二边短2acm，
（1）求此三角形的周长．
（2）当，时，求三角形的周长的值是多少？

某市为了节约用水，对自来水的收费标准作如下规定：每月每户用水不超过10吨的部分，按2元/吨收费；超过10吨的部分按2．5元/吨收费．
（1）若黄老师家5月份用水16吨，问应交水费多少元？
（2）若黄老师家7月用水a吨，问应交水费多少元？（用a的代数式表示）

某市区自2014年1月起，居民生活用水开始实行阶梯式计量水价，该阶梯式计量水价分为三级（如下表所示）：

月用水量（吨）	水价（元/吨）
第一级 20吨以下（含20吨）	1．6
第二级 20吨﹣30吨（含30吨）	2．4
第三级 30吨以上	3．2

 
例：某用户的月用水量为32吨，按三级计量应缴水费为：
1．6×20＋2．4×10＋3．2×2＝62．4（元）
（1）如果甲用户的月用水量为12吨，则甲需缴的水费为       元；
（2）如果乙用户缴的水费为39．2元，则乙月用水量         吨；
（3）如果丙用户的月用水量为a吨，则丙用户该月应缴水费多少元？（用含a的代数式表示，并化简）

某商场销售一种西装和领带，西装每套定价1000元，领带每条定价200元．“国庆节”
期间商场决定开展促销活动，活动期间向客户提供两种优惠方案．
方案一：买一套西装送一条领带；
方案二：西装和领带都按定价的90%付款．
现某客户要到该商场购买西装20套，领带x条（x＞20）．
（1）若该客户按方案一购买，需付款                 元．（用含x的代数式表示）
若该客户按方案二购买，需付款                 元．（用含x的代数式表示）
（2）若x=30，通过计算说明此时按（1）哪种方案购买较为合算？
（3）当x=30时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法．

如图，长方形的长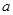为，宽为，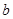

（1）用含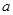、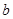的代数式表示右图阴影部分的面积S阴影．
（2）当a=5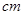，b=2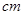时，求S阴影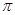．（取3．14）

如图，平面内有公共端点的6条射线O

A．O

B．O

C．O

D．OE、OF，按照图中的规律，从射线OA开始，按照逆时针方向，依次在射线上画点表示1，2，3，4，5，6，7，…

（1）根据图中规律，表示“19”的点在射线          上；
（2）按照图中规律推算，表示“2014”的点在射线          上；
（3）请你写出在射线OC上表示的数的规律（用含的代数式表示）                   ．

某餐厅中，一张桌子可坐6人，有以下两种摆放方式：
（1）当有张桌子时，两种摆放方式各能坐多少人？
（2）一天中午餐厅要接待98位顾客共同就餐，但餐厅只有25张这样的餐桌，若你是这个餐厅的经理，你打算选择哪种方式来摆放餐桌，为什么？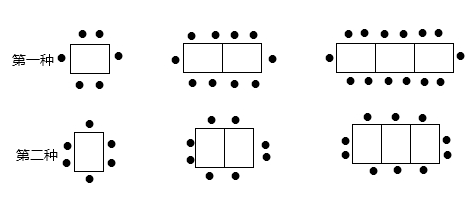

某服装厂生产一种西装和领带，西装每套定价200元，领带每条定价40元．厂方在开展促销活动期间，向客户提供两种优惠方案：
①买一套西装送一条领带；
②西装和领带都按定价的90%付款．
现某客户要到该服装厂购买西装20套，领带x条（x＞20）．
（1）若该客户按方案①购买，需付款                        元（用含x的代数式表示）；
若该客户按方案②购买，需付款                        元（用含x的代数式表示）；
（2）若x=30，通过计算说明此时按哪种方案购买较为合算？

扬州万家福商场将进货价80元的某品牌童装，以120元的销售价售出，平均每天能售出20件．则单件利润为120－80=40元，每天的盈利为40×20=800元．为了迎接“六一”儿童节，商场决定采取适当的降价措施．经调査，如果每件童装降价1元，那么平均每天就可多售出2件．（盈利=单件利润×销售量）
（1）若每件童装的销售价下降2元，则：
①降价后，每件童装的销售价为______________元；
②降价后，每件童装的利润为______________元；
③降价后，商场平均每天的销售量为__________________件．
（2）若设每件童装的销售价下降a元，试用含a的代数式填空：
①降价后，每件童装的销售价为______________元；
②降价后，每件童装的利润为______________元；
③降价后，商场平均每天的销售量为__________________件．
（3）如果商场要想平均每天销售这种童装盈利1200元．商场经理甲说“在原售价每件120元的基础上再下降20元，可以完成任务”，商场经理乙说“不用降那么多，在原售价每件120元的基础上再下降10元就可以了”，试判断经理甲与乙的说法是否正确，并说明理由．

操作与思考：
操作：将长为1，宽为的长方形纸片（），如图那样折一下，剪下一个边长等于长方形宽度的正方形（称为第一次操作）；再把剩下的长方形如图那样折一下，剪下一个边长等于此时长方形宽度的正方形（称为第二次操作）．如此反复操作下去，若在第n次操作后剩下的长方形是正方形，则操作终止．
思考：

（1）第一次操作后，剩下的长方形的边长分别为       、       ．（用含的式子表示）
（2）如果第二次操作后剩下的长方形恰好是正方形，则的值是              ．
（3）第三次操作后，若剩下的长方形恰好是正方形，试求的值．

一个三角形的第一条边长为（x＋2）cm，第二条边长比第一条边长小5cm，第三条边长是第二条边长的2倍．
（1）用含x的代数式表示这个三角形的周长；
（2）计算当x为6cm时这个三角形的周长．

有一长为240米的圆形跑道，小明和他的小狗同时从跑道的点P处出发沿顺时针方向跑步．已知小明的速度为4米/秒，小狗的速度为12米/秒．跑步的时间记为秒．在跑步过程中，小明和他的小狗之间相距（取两者之间较短一段圆弧跑道的长度）为米．
（1）当秒和秒时，分别求的值？
（2）当时，请用含的代数式表示．
（3）当时，请用含的代数式表示．（可直接写出结果）

某空调器销售商，今年四月份销出空调台，五月份销售空调比四月份的2倍多1台，六月份销售空调比前两个月的总和的4倍少15台．
（1）用代数式表示该销售商今年第二季度共销售空调多少台？
（2）当四月份销出空调为111台时，求第二季度销售的空调总数．

某城市大剧院地面的一部分为扇形，观众席的座位按下列方式设置：

排数	1	2	3	4
座位数	50	53	56	59

 
按这种方式排下去，
（1）第5、6排各有多少个座位？
（2）第n排有多少个座位？
（3）根据（2）的代数式，判断第25排有多少个座位？