重百商场正销售某品牌的一款等离子宽屏幕电视机,年初时售价定为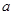 元,3月份售价降低了
元,3月份售价降低了 元.由于伦敦奥运会的举行,8月份销售看好,故商场决定将售价在3月份的基础上上涨10%.奥运会结束后,由于销售不畅,故商场决定将售价在8月份的基础上下调10%.
元.由于伦敦奥运会的举行,8月份销售看好,故商场决定将售价在3月份的基础上上涨10%.奥运会结束后,由于销售不畅,故商场决定将售价在8月份的基础上下调10%.
(1)请用代数式表示该款等离子宽屏幕电视机现在的价格;
(2)若年初时售价定为6500元,3月初售价降低了500元,那么该款等离子宽屏幕电视机现在的价格是多少元?
推荐套卷
重百商场正销售某品牌的一款等离子宽屏幕电视机,年初时售价定为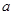 元,3月份售价降低了
元,3月份售价降低了 元.由于伦敦奥运会的举行,8月份销售看好,故商场决定将售价在3月份的基础上上涨10%.奥运会结束后,由于销售不畅,故商场决定将售价在8月份的基础上下调10%.
元.由于伦敦奥运会的举行,8月份销售看好,故商场决定将售价在3月份的基础上上涨10%.奥运会结束后,由于销售不畅,故商场决定将售价在8月份的基础上下调10%.
(1)请用代数式表示该款等离子宽屏幕电视机现在的价格;
(2)若年初时售价定为6500元,3月初售价降低了500元,那么该款等离子宽屏幕电视机现在的价格是多少元?