对于任意一个四位数 ,若千位上的数字与个位上的数字之和是百位上的数字与十位上的数字之和的2倍,则称这个四位数 为"共生数".例如: ,因为 ,所以3507是"共生数"; ,因为 ,所以4135不是"共生数".
(1)判断5313,6437是否为"共生数"?并说明理由;
(2)对于"共生数" ,当十位上的数字是千位上的数字的2倍,百位上的数字与个位上的数字之和能被9整除时,记 .求满足 各数位上的数字之和是偶数的所有 .
某矩形人行道由相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成,图1表示此人行道的地砖排列方式,其中正方形地砖为连续排列.
观察思考
当正方形地砖只有1块时,等腰直角三角形地砖有6块(如图 ;当正方形地砖有2块时,等腰直角三角形地砖有8块(如图 ;以此类推.

规律总结
(1)若人行道上每增加1块正方形地砖,则等腰直角三角形地砖增加 块;
(2)若一条这样的人行道一共有 为正整数)块正方形地砖,则等腰直角三角形地砖的块数为 (用含 的代数式表示).
问题解决
(3)现有2021块等腰直角三角形地砖,若按此规律再建一条人行道,要求等腰直角三角形地砖剩余最少,则需要正方形地砖多少块?
某书店新进了一批图书,甲、乙两种书的进价分别为4元 本、10元 本.现购进 本甲种书和 本乙种书,共付款 元.
(1)用含 , 的代数式表示 ;
(2)若共购进 本甲种书及 本乙种书,用科学记数法表示 的值.
“绿水青山就是金山银山”,为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向 , 两个果园运送有机化肥,甲、乙两个仓库分别可运出80吨和100吨有机化肥; , 两个果园分别需用110吨和70吨有机化肥.两个仓库到 , 两个果园的路程如表所示:
路程(千米) |
||
甲仓库 |
乙仓库 |
|
果园 |
15 |
25 |
果园 |
20 |
20 |
设甲仓库运往 果园 吨有机化肥,若汽车每吨每千米的运费为2元,
(1)根据题意,填写下表.
运量(吨 |
运费(元 |
|||
甲仓库 |
乙仓库 |
甲仓库 |
乙仓库 |
|
果园 |
|
|
|
|
果园 |
|
|
|
|
(2)设总运费为 元,求 关于 的函数表达式,并求当甲仓库运往 果园多少吨有机化肥时,总运费最省?最省的总运费是多少元?
若一个两位数十位、个位上的数字分别为,
,我们可将这个两位数记为
,易知
;同理,一个三位数、四位数等均可以用此记法,如
.
【基础训练】
(1)解方程填空:
①若,则
;
②若,则
;
③若,则
;
【能力提升】
(2)交换任意一个两位数的个位数字与十位数字,可得到一个新数
,则
一定能被 整除,
一定能被 整除,
一定能被 整除;(请从大于5的整数中选择合适的数填空)
【探索发现】
(3)北京时间2019年4月10日21时,人类拍摄的首张黑洞照片问世,黑洞是一种引力极大的天体,连光都逃脱不了它的束缚.数学中也存在有趣的黑洞现象:任选一个三位数,要求个、十、百位的数字各不相同,把这个三位数的三个数字按大小重新排列,得出一个最大的数和一个最小的数,用得出的最大的数减去最小的数得到一个新数(例如若选的数为325,则用,再将这个新数按上述方式重新排列,再相减,像这样运算若干次后一定会得到同一个重复出现的数,这个数称为“卡普雷卡尔黑洞数”.
①该“卡普雷卡尔黑洞数”为 ;
②设任选的三位数为(不妨设
,试说明其均可产生该黑洞数.
阅读下面的材料:
按照一定顺序排列着的一列数称为数列,数列中的每一个数叫做这个数列的项.排在第一位的数称为第一项,记为,排在第二位的数称为第二项,记为
,依此类推,排在第
位的数称为第
项,记为
.所以,数列的一般形式可以写成:
,
,
,
,
,
.
一般地,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列的公差,公差通常用表示.如:数列1,3,5,7,
为等差数列,其中
,
,公差为
.
根据以上材料,解答下列问题:
(1)等差数列5,10,15,的公差
为 ,第5项是 .
(2)如果一个数列,
,
,
,
,是等差数列,且公差为
,那么根据定义可得到:
,
,
,
,
,
.
所以
,
,
由此,请你填空完成等差数列的通项公式:
.
(3)是不是等差数列
,
,
的项?如果是,是第几项?
对任意一个四位数,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称
为“极数”.
(1)请任意写出三个“极数”;并猜想任意一个“极数”是否是99的倍数,请说明理由;
(2)如果一个正整数是另一个正整数
的平方,则称正整数
是完全平方数.若四位数
为“极数”,记
,求满足
是完全平方数的所有
.
对任意一个四位数,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称
为“极数”.
(1)请任意写出三个“极数”;并猜想任意一个“极数”是否是99的倍数,请说明理由;
(2)如果一个正整数是另一个正整数
的平方,则称正整数
是完全平方数.若四位数
为“极数”,记
,求满足
是完全平方数的所有
.
我们知道,任意一个正整数 都可以进行这样的分解: , 是正整数,且 ,在 的所有这种分解中,如果 , 两因数之差的绝对值最小,我们就称 是 的最佳分解.并规定: .例如12可以分解成 , 或 ,因为 ,所以 是12的最佳分解,所以 .
(1)如果一个正整数 是另外一个正整数 的平方,我们称正整数 是完全平方数.求证:对任意一个完全平方数 ,总有 ;
(2)如果一个两位正整数 , , , 为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数 为"吉祥数",求所有"吉祥数"中 的最大值.
我们知道,任意一个正整数 都可以进行这样的分解: , 是正整数,且 ,在 的所有这种分解中,如果 , 两因数之差的绝对值最小,我们就称 是 的最佳分解.并规定: .例如12可以分解成 , 或 ,因为 ,所以 是12的最佳分解,所以 .
(1)如果一个正整数 是另外一个正整数 的平方,我们称正整数 是完全平方数.求证:对任意一个完全平方数 ,总有 ;
(2)如果一个两位正整数 , , , 为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数 为"吉祥数",求所有"吉祥数"中 的最大值.
用边长为12cm的正方形硬纸板做三棱柱盒子,每个盒子的侧面为长方形,底面为等边三角形.
(1)每个盒子需 个长方形, 个等边三角形;
(2)硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)A方法:剪6个侧面;B方法:剪4侧面5个底面.
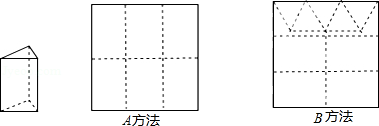
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
①用x的代数式分别表示裁剪出的侧面和底面的个数;
②若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
某城市为了鼓励居民节约用水,对自来水用户按如下标准收费:若每月每户用水的最高标准为10吨,超过标准的部分加价收费,不超过10吨,每吨按2.9元收费,超过10吨的部分按每吨4元收费,
(1)某用户3月份用水x吨,请用含x的代数式表示应交水费
(2)求当x=25时的水费.
将大小不同的两个正方形按如图所示那样拼接起来,连结BD、BF、DF,已知正方形ABCD的边长为 ,正方形CEFG的边长为
,正方形CEFG的边长为 ,且
,且 <
< .
.

(1)填空:BE×DG = (用含 、
、 的代数式表示);
的代数式表示);
(2)当正方形ABCD的边长 保持不变,而正方形CEFG的边长
保持不变,而正方形CEFG的边长 不断增大时,△BDF的面积会发生改变吗?请说明理由.
不断增大时,△BDF的面积会发生改变吗?请说明理由.
如图,一个点从数轴上的原点开始,先向左移动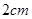 到达
到达 点,再向左移动
点,再向左移动 到达
到达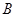 点,然后向右移动
点,然后向右移动 到达
到达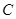 点.
点.
(1)用1个单位长度表示 ,请你在数轴上表示出
,请你在数轴上表示出 、
、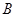 、
、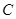 三点的位置;
三点的位置;
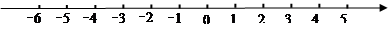
(2)把点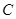 到点
到点 的距离记为
的距离记为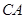 ,则
,则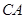 =
= 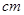 .
.
(3)阅读理解:观察式子: 因此可以得到:括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号.
因此可以得到:括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号.
问题解决
若点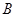 以每秒
以每秒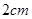 的速度向左移动,同时
的速度向左移动,同时 、
、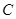 点分别以每秒
点分别以每秒 、
、 的速度向右移动.设移动时间为
的速度向右移动.设移动时间为 秒,试探索:
秒,试探索: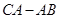 的值是否会随着
的值是否会随着 的变化而改变?请说明理由.
的变化而改变?请说明理由.