北京市延庆县第三协作区七年级上学期期中数学试卷
截止到2015年6月1日,北京市已建成34个地下调蓄设施,蓄水能力达到1 40 000立方平米. 将1 40 000用科学记数法表示应为( )
| A.14×104 | B.1.4×105 | C.1.4×106 | D.0.14×106 |
一条东西走向的道路上,小明先向西走3米,记作“-3米”,他又向西走了4米,此时小明的位置可记作( )
| A.-2米 | B.+7米 | C.-3米 | D.-7米 |
实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最大的是( )

| A.a | B.b | C.c | D.d |
有4盒小包装杨梅,每盒以标准克数(450克)为基准,超过的克数记作正数,不足的克数记作负数,以下数据是记录结果,其中表示实际克数最接近标准克数的是( )
| A.+2 | B.-3 | C.+3 | D. -1 |
全班同学排成长方形长队,每排的同学数为a,排数比每排同学数的3倍还多2,那么全班同学数是( )
A.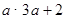 |
B. |
C.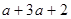 |
D.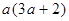 |
已知3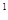 =3,3
=3,3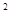 =9,3
=9,3 =27,3
=27,3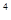 =81,3
=81,3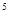 =243,3
=243,3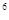 =729,3
=729,3 =2187,3
=2187,3 =6561…
=6561…
请你推测32014的个位数是( )
| A.1 | B.3 | C.7 | D.9 |
现定义某种运算“*”,对给定的两个有理数a、b(a≠0),有a*b=ab,则(-3)*2= .(计算出结果)
如图,平面内有公共端点的6条射线O
| A.O | B.O | C.O | D.OE、OF,按照图中的规律,从射线OA开始,按照逆时针方向,依次在射线上画点表示1,2,3,4,5,6,7,… |

(1)根据图中规律,表示“19”的点在射线 上;
(2)按照图中规律推算,表示“2014”的点在射线 上;
(3)请你写出在射线OC上表示的数的规律(用含 的代数式表示) .
的代数式表示) .
计算
(1)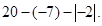
(2)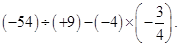
(3)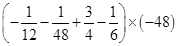
(4)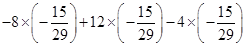
(5)(-1)3-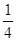 ×[2-(-3)
×[2-(-3)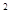 ]
]
(6)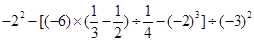
某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
| 与标准质量的差值(单位:克) |
-5 |
-2 |
0 |
1 |
3 |
6 |
| 袋 数 |
1 |
4 |
3 |
4 |
5 |
3 |
(1)这批样品的平均质量比标准质量多还是少?(通过计算方法来合理解释一下)
(2)若每袋标准质量为100克,则抽样检测的总质量是多少?
已知a,b互为相反数,c,d互为倒数,x的绝对值为5,试求:(a+b+cd)x2+(a+b)2008-(-cd)2015的值.
|
先阅读下面的解题过程,在解答后面的题目.
例:已知式子9-6y-4y2 =7,求2y2 +3y+7的值.解:由9-6y-4y2 =7得-6y-4y2=7-9,
即6y+4y2 =2,
故2y2 +3y=1,所以2y2 +3y+7=8.
题目:已知式子14x+5-21x2=-2,求6x2-4x+5的值.
阅读理解:
阅读下面材料:已知点A、B在数轴上分别表示有理数 、
、 ,A、B两点之间的距离表示为
,A、B两点之间的距离表示为 .当A、B两点中有一点在原点时,不妨设点A在原点,如图1,
.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,
当A、B两点都不在原点时,
(1)如图2,点A、B都在原点的右边,

(2)如图3,点A、B都在原点的左边,

(3)如图4,点A、B在原点的两边,

综上,数轴上A、B两点的距离

回答下列问题:
(1) 数轴上表示2和5两点之间的距离是_________.
数轴上表示-2和-5两点之间的距离是_________.
数轴上表示-1和3两点之间的距离是_________.
(2) 数轴上表示 和-1的两点A、B之间的距离是_________.
和-1的两点A、B之间的距离是_________.
如果 ,那么
,那么 为_________.
为_________.
(3) 当代数式 取最小值时,相应的x的取值范围是_________.
取最小值时,相应的x的取值范围是_________.
 的相反数是( ).
的相反数是( ).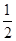
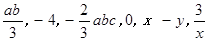 , 中,单项式有( )
, 中,单项式有( ) 与
与
 与
与
 与
与
 与
与


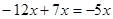

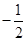
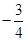 .(用“<”“>”连接)
.(用“<”“>”连接) 的系数是 ,次数是 .
的系数是 ,次数是 . 与
与 是同类项,则m=_________,n= .
是同类项,则m=_________,n= . 在数轴上的对应点如图所示,化简:
在数轴上的对应点如图所示,化简: .
.
 ,
, .
. ;
;  .
. ;
; ,其中
,其中 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号