如图,平面内有公共端点的6条射线O
| A.O | B.O | C.O | D.OE、OF,按照图中的规律,从射线OA开始,按照逆时针方向,依次在射线上画点表示1,2,3,4,5,6,7,… |
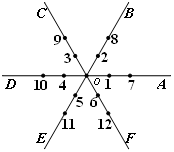
(1)根据图中规律,表示“19”的点在射线 上;
(2)按照图中规律推算,表示“2014”的点在射线 上;
(3)请你写出在射线OC上表示的数的规律(用含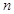 的代数式表示) .
的代数式表示) .
相关知识点
推荐套卷
如图,平面内有公共端点的6条射线O
| A.O | B.O | C.O | D.OE、OF,按照图中的规律,从射线OA开始,按照逆时针方向,依次在射线上画点表示1,2,3,4,5,6,7,… |

(1)根据图中规律,表示“19”的点在射线 上;
(2)按照图中规律推算,表示“2014”的点在射线 上;
(3)请你写出在射线OC上表示的数的规律(用含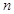 的代数式表示) .
的代数式表示) .