初中数学列代数式试题

某矩形人行道由相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成，图1表示此人行道的地砖排列方式，其中正方形地砖为连续排列．

$[$ 观察思考 $]$

当正方形地砖只有1块时，等腰直角三角形地砖有6块（如图 $2)$ ；当正方形地砖有2块时，等腰直角三角形地砖有8块（如图 $3)$ ；以此类推．

$[$ 规律总结 $]$

（1）若人行道上每增加1块正方形地砖，则等腰直角三角形地砖增加 　 　块；

（2）若一条这样的人行道一共有 $n(n$ 为正整数）块正方形地砖，则等腰直角三角形地砖的块数为 　　（用含 $n$ 的代数式表示）．

$[$ 问题解决 $]$

（3）现有2021块等腰直角三角形地砖，若按此规律再建一条人行道，要求等腰直角三角形地砖剩余最少，则需要正方形地砖多少块？

为了节约用水，某自来水公司采取以下收费方法：若每户每月用水不超过15吨，则每吨水收费2元；若每户每月用水超过15吨，则超过部分按每吨2.5元收费．9月份小明家用水a吨（a＞15吨）．
（1）请用代数式表示小明家9月份应交的水费；
（2）小明家9月份实际交水费50元，求小明家实际用水吨数？

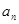如图，第（1）个多边形由正三角形“扩展”而来，边数记为，第（2）个多边形由正方形 “扩展”而来，边数记为，…，依此类推，由正边形“扩展”而来的多边形的边数记为（n≥3）．则的值是      ，当的结果是时，n的值         ．

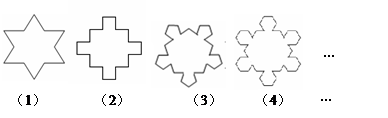
图（1）是一个长为 $2a$，宽为 $2b(a>b)$的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图（2）那样拼成一个正方形，则中间空余的部分的面积是 $($　　 $)$

A． $\mathit{ab}$B． ${(a+b)}^2$C． ${(a-b)}^2$D． $a^2-b^2$

某超市出售一商品，有如下四种在原标价基础上调价的方案，其中调价后售价最低的是 $($ 　　 $)$

A．	先打九五折，再打九五折	B．	先提价 $50\%$ ，再打六折
C．	先提价 $30\%$ ，再降价 $30\%$	D．	先提价 $25\%$ ，再降价 $25\%$

某地居民生活用水收费标准：每月用水量不超过17立方米，每立方米 $a$ 元；超过部分每立方米 $(a+1.2)$ 元．该地区某用户上月用水量为20立方米，则应缴水费为 $($ 　　 $)$

A．

$20a$ 元

B．

$(20a+24)$ 元

C．

$(17a+3.6)$ 元

D．

$(20a+3.6)$ 元

对于任意一个四位数 $m$ ，若千位上的数字与个位上的数字之和是百位上的数字与十位上的数字之和的2倍，则称这个四位数 $m$ 为"共生数"．例如： $m=3507$ ，因为 $3+7=2\times (5+0)$ ，所以3507是"共生数"； $m=4135$ ，因为 $4+5\ne 2\times (1+3)$ ，所以4135不是"共生数"．

（1）判断5313，6437是否为"共生数"？并说明理由；

（2）对于"共生数" $n$ ，当十位上的数字是千位上的数字的2倍，百位上的数字与个位上的数字之和能被9整除时，记 $F\left(n\right)=\frac{n}{3}$ ．求满足 $F\left(n\right)$ 各数位上的数字之和是偶数的所有 $n$ ．

已知苹果每千克 $m$元，则2千克苹果共多少元？ $($　　 $)$

A． $m-2$B． $m+2$C． $\frac{m}{2}$D． $2m$

“绿水青山就是金山银山”，为了保护环境和提高果树产量，某果农计划从甲、乙两个仓库用汽车向 $A$， $B$两个果园运送有机化肥，甲、乙两个仓库分别可运出80吨和100吨有机化肥； $A$， $B$两个果园分别需用110吨和70吨有机化肥．两个仓库到 $A$， $B$两个果园的路程如表所示：

	路程（千米）
	甲仓库	乙仓库
$A$果园	15	25
$B$果园	20	20

设甲仓库运往 $A$果园 $x$吨有机化肥，若汽车每吨每千米的运费为2元，

（1）根据题意，填写下表．

	运量（吨 $)$		运费（元 $)$
	甲仓库	乙仓库	甲仓库	乙仓库
$A$果园	$x$	$110-x$	$2\times 15x$	$2\times 25(110-x)$
$B$果园

（2）设总运费为 $y$元，求 $y$关于 $x$的函数表达式，并求当甲仓库运往 $A$果园多少吨有机化肥时，总运费最省？最省的总运费是多少元？

某水果店销售50千克香蕉，第一天售价为9元 $/$千克，第二天降价为6元 $/$千克，第三天再降为3元 $/$千克．三天全部售完，共计所得270元．若该店第二天销售香蕉 $t$千克，则第三天销售香蕉　　千克．（用含 $t$的代数式表示． $)$

将 $x$ 克含糖 $10\%$ 的糖水与 $y$ 克含糖 $30\%$ 的糖水混合，混合后的糖水含糖 $($ 　　 $)$

A．	$20\%$	B．	$\frac{x+y}{2}\times 100\%$
C．	$\frac{x+3y}{20}\times 100\%$	D．	$\frac{x+3y}{10x+10y}\times 100\%$

如图，将边长为 $3a$的正方形沿虚线剪成两块正方形和两块长方形．若拿掉边长 $2b$的小正方形后，再将剩下的三块拼成一块矩形，则这块矩形较长的边长为 $($　　 $)$

A． $3a+2b$B． $3a+4b$C． $6a+2b$D． $6a+4b$

用代数式表示： $a$的2倍与3的和．下列表示正确的是 $($　　 $)$

A． $2a-3$B． $2a+3$C． $2(a-3)$D． $2(a+3)$

苹果原价是每斤 $a$元，现在按8折出售，假如现在要买一斤，那么需要付费 $($　　 $)$

A． $0.8a$元B． $0.2a$元C． $1.8a$元D． $(a+0.8)$元

如图是一个长为 $a$，宽为 $b$的矩形，两个阴影图形都是一对底边长为1，且底边在矩形对边上的平行四边形．

（1）用含字母 $a$， $b$的代数式表示矩形中空白部分的面积；

（2）当 $a=3$， $b=2$时，求矩形中空白部分的面积．